题目内容
两座灯塔A和B与海洋观察站C的距离都等于a Km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为______km．
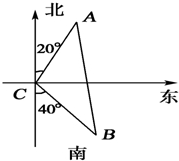
根据题意，得
△ABC中，∠ACB=180°-20°-40°=120°，
∵AC=BC=akm
∴由余弦定理，得cos120°=
即-
=
，解之得AB=
a（舍负）
即灯塔A与灯塔B的距离为
akm
故答案为：
a
△ABC中，∠ACB=180°-20°-40°=120°，
∵AC=BC=akm
∴由余弦定理，得cos120°=
| AB2+BC2-AB2 |
| 2AB×BC |
即-
| 1 |
| 2 |
| a2+a2-AB2 |
| 2×a×a |
| 3 |
即灯塔A与灯塔B的距离为
| 3 |
故答案为：
| 3 |
练习册系列答案
优质课堂快乐成长系列答案
相关题目
的值；
，求
的值