题目内容
(文)如图,在Rt△ABC中,已知BC=a,若长为2a的线段PQ以点A为中点,问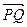 与
与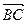 的夹角θ取何值时,
的夹角θ取何值时,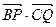 的值最大?并求出这个最大值。
的值最大?并求出这个最大值。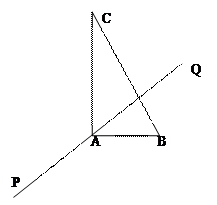

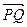 与
与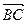 的夹角θ取何值时,
的夹角θ取何值时,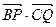 的值最大?并求出这个最大值。
的值最大?并求出这个最大值。

解:






A为PQ的中点,

 =0+(
=0+( )
)
 -a2=
-a2= - a2= -a2cosθ-a2
- a2= -a2cosθ-a2
故当θ=0°时最 大,最大值为0.
大,最大值为0.
思路二:以A为坐标原点以AB为x轴建立直角坐标系,则B(b,0),C(0,c),b2+c2=a2
设P(x,y)则Q点(-x,-y),x2+y2=a2
 ,
,
 =-x2-y2+bx-cy=
=-x2-y2+bx-cy= -a2=a2cosθ-a2
-a2=a2cosθ-a2
下同前.






A为PQ的中点,


 =0+(
=0+( )
)
 -a2=
-a2= - a2= -a2cosθ-a2
- a2= -a2cosθ-a2故当θ=0°时最
 大,最大值为0.
大,最大值为0.思路二:以A为坐标原点以AB为x轴建立直角坐标系,则B(b,0),C(0,c),b2+c2=a2
设P(x,y)则Q点(-x,-y),x2+y2=a2
 ,
,
 =-x2-y2+bx-cy=
=-x2-y2+bx-cy= -a2=a2cosθ-a2
-a2=a2cosθ-a2下同前.
略

练习册系列答案
相关题目
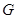 是△
是△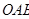 的重心,
的重心,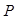 、
、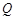 分别是边
分别是边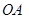 、
、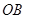 上的动点,且
上的动点,且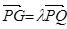 ,将
,将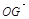 用
用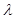 、
、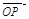 、
、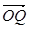 表示;
表示;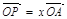 ,
,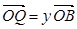 ,证明:
,证明: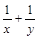 是定值;
是定值;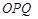 的面积分别为
的面积分别为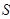 、
、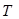 .求
.求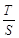 的取值范围.
的取值范围.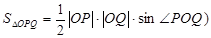
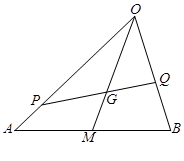
 ,当
,当 时,有
时,有 〈 0 恒成立,求实数m
〈 0 恒成立,求实数m 的取值范围.
的取值范围. 中,点P是AB上一点,且
中,点P是AB上一点,且 , Q是BC中点,AQ与
, Q是BC中点,AQ与 ,则
,则 的值为 ( )
的值为 ( )



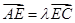 。又以A、B为焦点的双曲线过C、D、E三点。若
。又以A、B为焦点的双曲线过C、D、E三点。若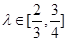 ,则双曲线离心率e的取值范围为( )
,则双曲线离心率e的取值范围为( )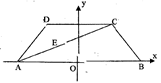
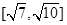 B.
B.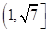 C.
C. D.
D.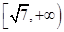
 中,点
中,点 是
是 中点。过点
中点。过点 、
、 于不同两点
于不同两点 、
、 。若
。若 ,则
,则 的值W为
的值W为 
 的图像的一条对
的图像的一条对 称轴为
称轴为
 为方向向量的直线的倾斜角为
为方向向量的直线的倾斜角为  的值为
的值为  为椭圆
为椭圆 上任意一点,
上任意一点, 为线段
为线段 的中点,求
的中点,求 的最小值 。
的最小值 。