题目内容
在 中,点P是AB上一点,且
中,点P是AB上一点,且 , Q是BC中点,AQ与
, Q是BC中点,AQ与
CP交点为M,又 ,则
,则 的值为 ( )
的值为 ( )
 中,点P是AB上一点,且
中,点P是AB上一点,且 , Q是BC中点,AQ与
, Q是BC中点,AQ与CP交点为M,又
 ,则
,则 的值为 ( )
的值为 ( )A. | B. | C. | D. |
D
先根据向量关系 得即P是AB的一个
得即P是AB的一个 三等分点,利用平面几何知识,过点Q作PC的平行线交AB于D,利用三角形的中位线定理得到PC=4PM,
三等分点,利用平面几何知识,过点Q作PC的平行线交AB于D,利用三角形的中位线定理得到PC=4PM,
结合向量条件即可求得t值.
解:∵

∴
∴ 即P是AB的一个三等分点,
即P是AB的一个三等分点,
过点Q作PC的平行线交AB于D,
∵Q是BC中点,∴QD= PC,且D是PB的中点,
PC,且D是PB的中点,
从而QD=2PM,
∴PC=4PM,
∴CM=
又 ,则t=
,则t=
故选D.
 得即P是AB的一个
得即P是AB的一个 三等分点,利用平面几何知识,过点Q作PC的平行线交AB于D,利用三角形的中位线定理得到PC=4PM,
三等分点,利用平面几何知识,过点Q作PC的平行线交AB于D,利用三角形的中位线定理得到PC=4PM,结合向量条件即可求得t值.
解:∵


∴

∴
 即P是AB的一个三等分点,
即P是AB的一个三等分点,过点Q作PC的平行线交AB于D,
∵Q是BC中点,∴QD=
 PC,且D是PB的中点,
PC,且D是PB的中点,从而QD=2PM,
∴PC=4PM,
∴CM=

又
 ,则t=
,则t=
故选D.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
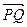 与
与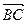 的夹角θ取何值时,
的夹角θ取何值时,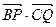 的值最大?并求出这个最大值。
的值最大?并求出这个最大值。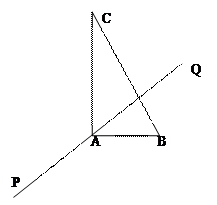

 =
= +
+ ,(t为实数);
,(t为实数);



 中,
中, 是
是 的中点,
的中点, ,点
,点 在
在 上,且满足
上,且满足 ,则
,则




 (
( 为正常数),点
为正常数),点 在
在 轴的负半轴上,点
轴的负半轴上,点 在
在 轴上,且
轴上,且 ,
, .
.  轴上运动时,求点
轴上运动时,求点 的轨迹
的轨迹 的方程;
的方程; 过点
过点 且与曲线
且与曲线 ,分别过点
,分别过点 :
: 的
的 垂线,对应的垂足分别为
垂线,对应的垂足分别为
 ,求
,求 的值;
的值; ,
, ,
, ,
, ,求
,求 的值.
的值.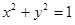 上三点,且
上三点,且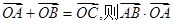 = .
= . 满足
满足 ,则
,则 的最大值等于
的最大值等于

 中,若
中,若 ,则
,则