题目内容
如图,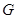 是△
是△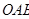 的重心,
的重心,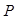 、
、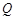 分别是边
分别是边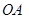 、
、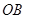 上的动点,且
上的动点,且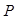 、
、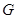 、
、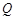 三点共线.
三点共线.
(1)设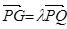 ,将
,将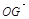 用
用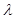 、
、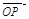 、
、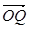 表示;
表示;
(2)设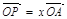 ,
,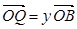 ,证明:
,证明: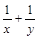 是定值;
是定值;
(3)记△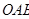 与△
与△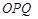 的面积分别为
的面积分别为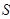 、
、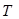 .求
.求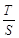 的取值范围.
的取值范围.
(提示: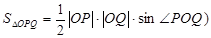
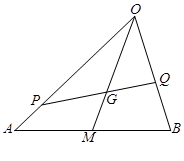
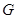 是△
是△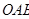 的重心,
的重心,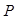 、
、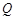 分别是边
分别是边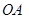 、
、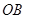 上的动点,且
上的动点,且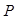 、
、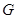 、
、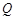 三点共线.
三点共线.(1)设
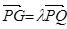 ,将
,将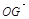 用
用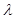 、
、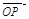 、
、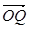 表示;
表示;(2)设
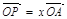 ,
,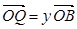 ,证明:
,证明: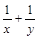 是定值;
是定值;(3)记△
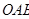 与△
与△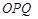 的面积分别为
的面积分别为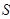 、
、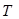 .求
.求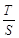 的取值范围.
的取值范围.(提示:
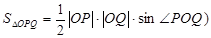
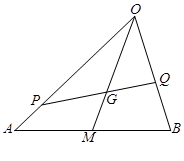
(1)
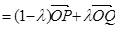 . (2)
. (2)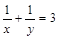 (定值).(3)
(定值).(3)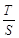 的取值范围
的取值范围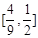

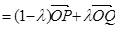 . (2)
. (2)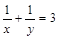 (定值).(3)
(定值).(3)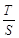 的取值范围
的取值范围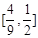
第一问中利用(1)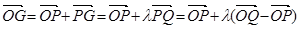
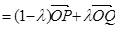
第二问中,由(1),得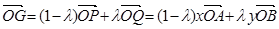 ;①
;①
另一方面,∵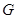 是△
是△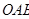 的重心,
的重心,
∴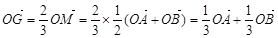
而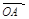 、
、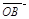 不共线,∴由①、②,得
不共线,∴由①、②,得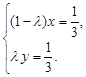
第三问中,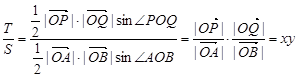
由点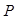 、
、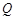 的定义知
的定义知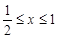 ,
,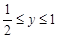 ,
,
且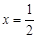 时,
时,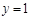 ;
;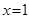 时,
时,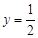 .此时,均有
.此时,均有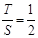 .
.
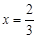 时,
时,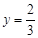 .此时,均有
.此时,均有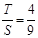 .
.
以下证明: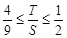 ,结合作差法得到。
,结合作差法得到。
解:(1)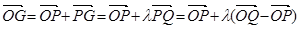
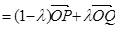 .
.
(2)一方面,由(1),得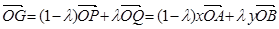 ;①
;①
另一方面,∵ 是△
是△ 的重心,
的重心,
∴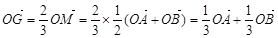 . ②
. ②
而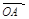 、
、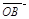 不共线,∴由①、②,得
不共线,∴由①、②,得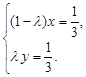
解之,得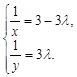 ,∴
,∴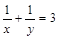 (定值).
(定值).
(3)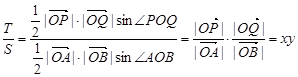 .
.
由点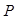 、
、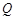 的定义知
的定义知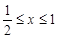 ,
,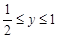 ,
,
且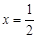 时,
时,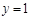 ;
;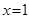 时,
时,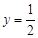 .此时,均有
.此时,均有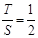 .
.
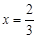 时,
时,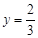 .此时,均有
.此时,均有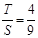 .
.
以下证明: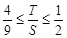 .(法一)由(2)知
.(法一)由(2)知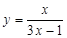 ,
,
∵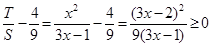 ,∴
,∴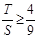 .
.
∵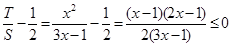 ,∴
,∴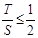 .
.
∴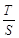 的取值范围
的取值范围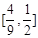
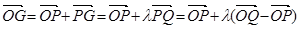
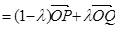
第二问中,由(1),得
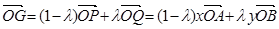 ;①
;① 另一方面,∵
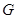 是△
是△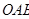 的重心,
的重心,∴
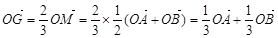
而
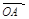 、
、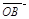 不共线,∴由①、②,得
不共线,∴由①、②,得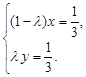
第三问中,
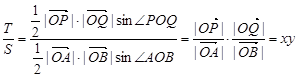
由点
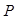 、
、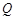 的定义知
的定义知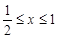 ,
,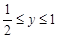 ,
,且
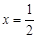 时,
时,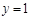 ;
;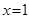 时,
时,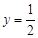 .此时,均有
.此时,均有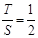 .
.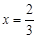 时,
时,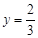 .此时,均有
.此时,均有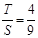 .
.以下证明:
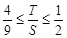 ,结合作差法得到。
,结合作差法得到。解:(1)
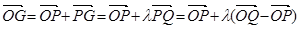
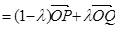 .
. (2)一方面,由(1),得
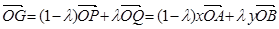 ;①
;① 另一方面,∵
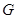 是△
是△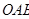 的重心,
的重心,∴
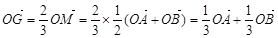 . ②
. ② 而
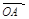 、
、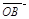 不共线,∴由①、②,得
不共线,∴由①、②,得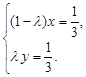
解之,得
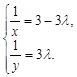 ,∴
,∴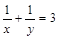 (定值).
(定值).(3)
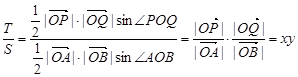 .
.由点
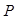 、
、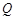 的定义知
的定义知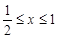 ,
,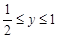 ,
,且
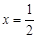 时,
时,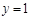 ;
;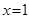 时,
时,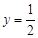 .此时,均有
.此时,均有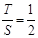 .
.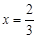 时,
时,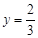 .此时,均有
.此时,均有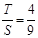 .
.以下证明:
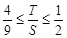 .(法一)由(2)知
.(法一)由(2)知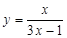 ,
,∵
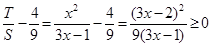 ,∴
,∴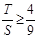 .
. ∵
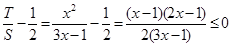 ,∴
,∴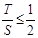 .
.∴
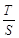 的取值范围
的取值范围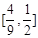

练习册系列答案
相关题目
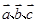 两两之间的夹角为60°,其模长都为1,则|
两两之间的夹角为60°,其模长都为1,则| 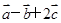 |等于
|等于 向量
向量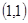 向上向左均平移1个单位后所得向量为 ;
向上向左均平移1个单位后所得向量为 ;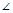 A=90°,AB=1,设点P,Q满足
A=90°,AB=1,设点P,Q满足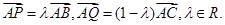 若
若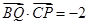 ,则
,则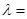



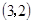 ,若点N
,若点N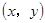 满足不等式组
满足不等式组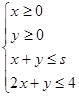 ,当
,当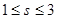 时,则
时,则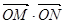 的最大值的变化范围是( )
的最大值的变化范围是( )


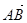 ·
·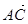 =-2,则|
=-2,则|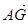 |的最小值是 .
|的最小值是 .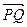 与
与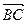 的夹角θ取何值时,
的夹角θ取何值时,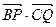 的值最大?并求出这个最大值。
的值最大?并求出这个最大值。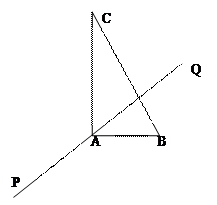

 夹角为
夹角为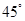 ,且
,且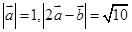 ;则
;则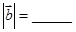
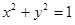 上三点,且
上三点,且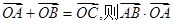 = .
= .