题目内容
在正方体ABCDA1B1C1D1中,M为DD1的中点,O为四边形ABCD的中心,P为棱A1B1上任一点,则异面直线OP与MA所成的角为
- A.30°
- B.45°
- C.60°
- D.90°
D
分析:根据题意,直线OP在点O与A1B1确定的平面内.设点O与A1B1确定的平面为α,α∩AD=F且α∩BC=E,可得F、E为AD、BC的中点,由正方形的性质可得AM⊥A1F,由A1B1⊥面ADD1A1可得A1B1⊥AM.因此AM⊥面A1FEB1,结合OP?面A1FEB1得AM⊥OP.由此即可得到异面直线OP与MA所成的角为90°.
解答:∵A1B1⊥面ADD1A1,AM?面ADD1A1, ∴A1B1⊥AM.
∴A1B1⊥AM.
设点O与A1B1确定的平面为α,α∩AD=F且α∩BC=E,则F、E为AD、BC的中点,
根据正方形的性质,可得AM⊥A1F.
∵A1F∩A1B1=A1,A1F、A1B1?平面面A1FEB1,∴AM⊥面A1FEB1,
又∵OP?面A1FEB1,∴AM⊥OP.
即直线OP与直线AM所成的角是90°.
故选:D
点评:本题在正方体中求异面直线所成角的大小,着重考查了线面垂直的判定与性质、正方体的结构特征等知识,属于基础题.
分析:根据题意,直线OP在点O与A1B1确定的平面内.设点O与A1B1确定的平面为α,α∩AD=F且α∩BC=E,可得F、E为AD、BC的中点,由正方形的性质可得AM⊥A1F,由A1B1⊥面ADD1A1可得A1B1⊥AM.因此AM⊥面A1FEB1,结合OP?面A1FEB1得AM⊥OP.由此即可得到异面直线OP与MA所成的角为90°.
解答:∵A1B1⊥面ADD1A1,AM?面ADD1A1,
 ∴A1B1⊥AM.
∴A1B1⊥AM.设点O与A1B1确定的平面为α,α∩AD=F且α∩BC=E,则F、E为AD、BC的中点,
根据正方形的性质,可得AM⊥A1F.
∵A1F∩A1B1=A1,A1F、A1B1?平面面A1FEB1,∴AM⊥面A1FEB1,
又∵OP?面A1FEB1,∴AM⊥OP.
即直线OP与直线AM所成的角是90°.
故选:D
点评:本题在正方体中求异面直线所成角的大小,着重考查了线面垂直的判定与性质、正方体的结构特征等知识,属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 +
+ =1(a>b>0)的右焦点为圆心的圆经过原点,且被椭圆的右准线分成弧长为2:1的两段弧,那么该椭圆的离心率等于________.
=1(a>b>0)的右焦点为圆心的圆经过原点,且被椭圆的右准线分成弧长为2:1的两段弧,那么该椭圆的离心率等于________.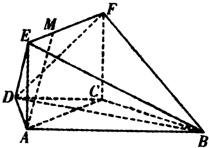 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上. ,该研究性学习小组又分成两个小组进行验证性实验.
,该研究性学习小组又分成两个小组进行验证性实验. ,且2∈A,3∉A,则实数a的取值范围是________.
,且2∈A,3∉A,则实数a的取值范围是________.



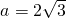 ,c=4,A=60°,则b=________.
,c=4,A=60°,则b=________.