题目内容
在△ABC中，若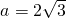 
，c=4，A=60°，则b=________．
2
分析：在△ABC中，由余弦定理可得 12=16+b2-8bcos60°，解方程求得 b 的值．
解答：在△ABC中，由余弦定理可得 12=16+b2-8bcos60°=16+b2-4b，
∴b=2，故答案为：2．
点评：本题考查余弦定理的应用，得到 12=16+b2-8bcos60°，是解题的关键．
分析：在△ABC中，由余弦定理可得 12=16+b2-8bcos60°，解方程求得 b 的值．
解答：在△ABC中，由余弦定理可得 12=16+b2-8bcos60°=16+b2-4b，
∴b=2，故答案为：2．
点评：本题考查余弦定理的应用，得到 12=16+b2-8bcos60°，是解题的关键．
练习册系列答案
轻松暑假总复习系列答案
相关题目
在△ABC中，若acosA=bcosB，则△ABC的形状是（ ）
| A、等腰三角形 | B、直角三角形 | C、等腰直角三角形 | D、等腰或直角三角形 |
在△ABC中，若sinB=
，cosC=
，则cosA的值是（ ）
| 4 |
| 5 |
| 12 |
| 13 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|