题目内容
20.已知直线l1是抛物线C:y2=8x的准线,P是C上的一动点,则P到直线l1与直线l2:3x-4y+24=0的距离之和的最小值为( )| A. | $\frac{24}{5}$ | B. | $\frac{26}{5}$ | C. | 6 | D. | $\frac{32}{5}$ |
分析 由题意可知:点P到直线3x-4y+24=0的距离为丨PA丨,点P到x=-2的距离为丨PB丨,则点P到直线l2:3x-4y+24=0和x=-2的距离之和为丨PF丨+丨PB丨,当A,P和F共线时,点P到直线l2:3x-4y+24=0和直线x=-2的距离之和的最小,利用点到直线的距离公式,即可求得答案.
解答 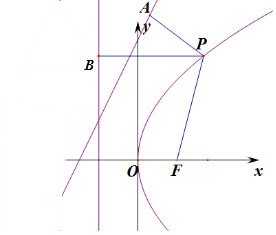 解:由抛物线的方程,焦点F(2,0),
解:由抛物线的方程,焦点F(2,0),
准线方程x=-2,根据题意作图如右图,
点P到直线l2:3x-4y+24=0的距离为丨PA丨,
点P到x=-2的距离为丨PB丨;
而由抛物线的定义知:丨PB丨=丨PF丨,
故点P到直线l2:3x-4y+24=0和x=-2的距离之和为
丨PF丨+丨PA丨,
而点F(2,0),到直线l2:3x-4y+24=0的距离为$\frac{|6+24|}{\sqrt{{3}^{2}+(-4)^{2}}}$=6,
P到直线l2:3x-4y+24=0和直线x=-2的距离之和的最小值:6,
故选:C.
点评 本题考查抛物线的定义的应用及简单几何性质,考查点到直线的距离公式,考查计算能力,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
10.直线$y=\sqrt{3}x+2$的倾斜角是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
11.若tanα=2,则$\frac{sinα+cosα}{sinα-cosα}$+cos2α的值为( )
| A. | $\frac{7}{4}$ | B. | -$\frac{14}{5}$ | C. | $\frac{16}{5}$ | D. | $\frac{15}{4}$ |
 如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=6,E是PB的动点.
如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=6,E是PB的动点.