题目内容
在如图所示的空间几何体中,平面![]() 平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在
平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在![]() 的平分线上。
的平分线上。
(1)求证:DE//平面ABC; (2)求二面角E—BC—A的余弦;
(3)求多面体ABCDE的体积。
解:方法一:(1)由题意知, ![]() 都是边长为2的等边三角形,
都是边长为2的等边三角形,
 取AC中点O,连接BO,DO,
取AC中点O,连接BO,DO,
则![]()
![]() 平面ACD
平面ACD![]() 平面ABC
平面ABC
![]() 平面ABC,作EF
平面ABC,作EF![]() 平面ABC,
平面ABC,
那么EF//DO,根据题意,点F落在BO上,
![]() ,易求得
,易求得![]()
所以四边形DEFO是平行![]() 四边形,DE//OF;
四边形,DE//OF;
![]() 平面ABC,
平面ABC,![]() 平面ABC,
平面ABC,
![]() 平面ABC
平面ABC
(2)作FG![]() BC,垂足为G,连接EG;
BC,垂足为G,连接EG;
![]() 平面ABC,根据三垂线定理可知,EG
平面ABC,根据三垂线定理可知,EG![]() BC
BC
![]() 就是二面角E—BC—A的平面角
就是二面角E—BC—A的平面角
![]()
![]()

![]()
即二面角E—BC—A的余弦值为![]()
(3)![]() 平面ACD
平面ACD![]() 平面ABC,OB
平面ABC,OB![]() AC
AC
![]() 平面ACD;又
平面ACD;又![]()
![]() 平面DAC,
平面DAC,![]() 三棱锥E—DAC的体积
三棱锥E—DAC的体积
![]()
又三![]() 棱锥E—ABC的体积
棱锥E—ABC的体积![]() [来源:Zxxk.Com]
[来源:Zxxk.Com]
![]() 多面体DE—ABC的体积为V=V1-V2=
多面体DE—ABC的体积为V=V1-V2=![]() …………13分
…………13分
方法二:(1)同方法一
(2)建立![]() 如图所示的空间直角坐标系
如图所示的空间直角坐标系![]() ,
,
可求得平面ABC的一个法向量为![]() ,
,
平面BCE的一个法向量为![]()
所以
![]()
又由图知,所求二面角的平面角是锐角,所以二面角E—BC—A的余弦值为![]()

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
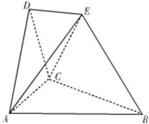 在如图所示的空间几何体中,△ABC,△ACD都是等边三角形,AE=CE,DE∥平面ABC,平面ACD⊥平面ABC.
在如图所示的空间几何体中,△ABC,△ACD都是等边三角形,AE=CE,DE∥平面ABC,平面ACD⊥平面ABC.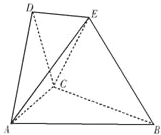 在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.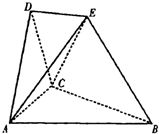 在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.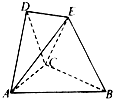 在如图所示的空间几何体中,平面ACD⊥平面ABC.BE和平面ABC所成的角为
在如图所示的空间几何体中,平面ACD⊥平面ABC.BE和平面ABC所成的角为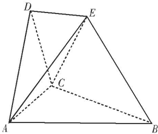 在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.