题目内容
15.函数y=3${\;}^{\sqrt{x-2}}}$的值域为[1,+∞).分析 根据复合函数的性质,求解出u=$\sqrt{x-2}$的值域,再求解y=3u的值域即可.
解答 解:函数y=3${\;}^{\sqrt{x-2}}}$,
令u=$\sqrt{x-2}$,可知u≥0,
∴函数y=3u是增函数,在区间[0,+∞)是单调递增.
当u=0时,y取得最小值为1.
∴函数y=3${\;}^{\sqrt{x-2}}}$的值域为[1,+∞)
故答案为[1,+∞)
点评 本题考查了分段函数的值域的求法.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.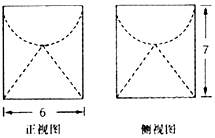 某几何体由圆柱挖掉半个球和一个圆锥所得,三视图中的正视图和侧视图如图所示,求该几何体的表面积( )
某几何体由圆柱挖掉半个球和一个圆锥所得,三视图中的正视图和侧视图如图所示,求该几何体的表面积( )
 某几何体由圆柱挖掉半个球和一个圆锥所得,三视图中的正视图和侧视图如图所示,求该几何体的表面积( )
某几何体由圆柱挖掉半个球和一个圆锥所得,三视图中的正视图和侧视图如图所示,求该几何体的表面积( )| A. | 60π | B. | 75π | C. | 90π | D. | 93π |
6.化简$\sqrt{1-{{sin}^2}{{140}°}}$=( )
| A. | ±cos40° | B. | cos40° | C. | -cos40° | D. | ±|cos40°| |
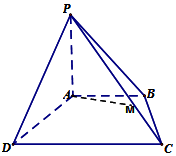 四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°.
四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°.