Question

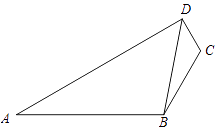
【题目】如图，已知A，B，C，D四点共面，且CD=1，BC=2，AB=4，∠ABC=120°，cos∠BDC= ．

（1）求sin∠DBC；
（2）求AD．

Answer 1

【答案】
（1）解：在△BDC中，因为 ，

所以 ．

由正弦定理 得， ．

（2）解：在△BDC中，由BC2=DC2+DB2﹣2DCDBcos∠BDC，

得， ．

所以 ．

解得 或 （舍）．

由已知得∠DBC是锐角，又 ，

所以 ．

所以cos∠ABD=cos（120°﹣∠DBC）=cos120°cos∠DBC+sin120°sin∠DBC= = ．

在△ABD中，因为AD2=AB2+BD2﹣2ABBDcos∠ABD= ，

所以 ．

【解析】（1）利用已知及同角三角函数基本关系式可求 ，进而利用正弦定理即可求得sin∠DBC的值．（2）在△BDC中，由余弦定理可求DB的值，利用同角三角函数基本关系式可求 ，进而利用两角差的余弦函数公式可求cos∠ABD的值，在△ABD中，由余弦定理可求AD的值．
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识，掌握正弦定理:，以及对余弦定理的定义的理解，了解余弦定理:;;．