题目内容
已知P为△ABC内一点，且3
+4
+5
=0.延长AP交BC于点D，若
=a，
=b，用a、b表示向量
、
．
| AP |
| BP |
| CP |
| AB |
| AC |
| AP |
| AD |
∵
=
-
=
-a，
=
-
=
-b，
又3
+4
+5
=0，
∴3
+4(
-a)+5(
-b)=0，
化简，得
=
a+
b．
设
=t
（t∈R），
则
=
ta+
tb．①
又设
=k
（k∈R），由
=
-
=b-a，得
=k（b-a）．而
=
+
=a+
，
∴
=a+k（b-a）=（1-k）a+kb．②
由①②，得
解得t=
.
代入①，有
=
a+
b．
| BP |
| AP |
| AB |
| AP |
| CP |
| AP |
| AC |
| AP |
又3
| AP |
| BP |
| CP |
∴3
| AP |
| AP |
| AP |
化简，得
| AP |
| 1 |
| 3 |
| 5 |
| 12 |
设
| AD |
| AP |
则
| AD |
| 1 |
| 3 |
| 5 |
| 12 |
又设
| BD |
| BC |
| BC |
| AC |
| AB |
| BD |
| AD |
| AB |
| BD |
| BD |
∴
| AD |
由①②，得
|
| 4 |
| 3 |
代入①，有
| AD |
| 4 |
| 9 |
| 5 |
| 9 |
练习册系列答案
相关题目
已知O为平面内一定点，设条件p：动点M满足
=
+λ（
+
），λ∈R；条件q：点M的轨迹通过△ABC的重心．则条件p是条件q的（ ）
| OM |
| OA |
| AB |
| AC |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
=
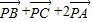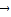，现随机将一颗豆子撒在△ABC内，则豆子落在△PBC内的概率为 ．
=
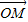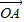+λ（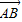
+
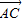），λ∈R；条件q：点M的轨迹通过△ABC的重心．则条件p是条件q的（ ）