题目内容
在四棱锥V—ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.(1)证明AB⊥平面VAD;
(2)求面VAD与面VDB所成二面角的大小.
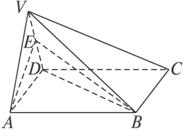
(1)证明:
![]() AB⊥平面VAD.
AB⊥平面VAD.
(2)解:取VD的中点E,连结EA、EB.
∵△VAD是正三角形,
∴AE=![]() AD,AE⊥VD.
AD,AE⊥VD.
∵AB⊥平面VAD,∴AB⊥AE.
又由三垂线定理知BE⊥VD,
因此,∠AEB是所求二面角的平面角.
于是tan∠AEB=![]() ,
,
∴所求二面角的大小为arctan![]() .
.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
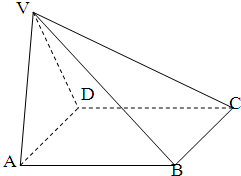 如图,在四棱锥V-ABCD中底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD
如图,在四棱锥V-ABCD中底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD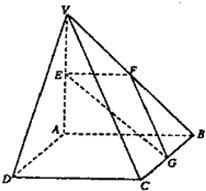 如图,在四棱锥V-ABCD中,底面ABCD是矩形,侧棱VA⊥底面ABCD,E、F、G分别为VA、VB、BC的中点.
如图,在四棱锥V-ABCD中,底面ABCD是矩形,侧棱VA⊥底面ABCD,E、F、G分别为VA、VB、BC的中点.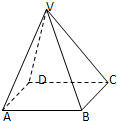 如图:在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为
如图:在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为 在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.