题目内容
在正方体 中,点
中,点 是上底面
是上底面 的中心,点
的中心,点 在线段
在线段 上运动,则异面直线
上运动,则异面直线 与
与 所成角
所成角 最大时,
最大时, .
.

【解析】
试题分析:根据题意,画出正方体 ,异面直线
,异面直线 与
与 所成的角为
所成的角为 与
与 所成的角,当点
所成的角,当点 与点
与点 重合时,所求异面直线所成角此时为
重合时,所求异面直线所成角此时为 ,当点
,当点 与点
与点 重合时,所求异面直线即为
重合时,所求异面直线即为 ,设正方体的边长为
,设正方体的边长为 ,在
,在 中,
中, ,所以
,所以 ,所以动点
,所以动点 从
从 点出发,沿着
点出发,沿着 移动,所求异面直线所成角越来越大,当到达点
移动,所求异面直线所成角越来越大,当到达点 时达到最大,所以
时达到最大,所以
 .
.
考点:1.空间几何体中异面直线所成角;2.三角形的余弦定理.

练习册系列答案
相关题目
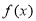 是定义在实数集
是定义在实数集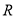 上的不恒为零的偶函数,且对任意实数
上的不恒为零的偶函数,且对任意实数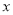 都有
都有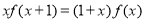 ,则
,则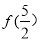 的值是
的值是 C.1 D.
C.1 D.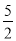
 ,集合
,集合  ,则
,则  等于( )
等于( ) 值是 ()
值是 ()
 的前
的前 项和为
项和为 ,向量
,向量 ,
, ,满足条件
,满足条件 ,
, 且
且 .
. ,数列
,数列 满足条件
满足条件 ,
,
 ,求数列
,求数列 的前
的前 和
和 .
.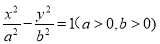 的左右焦点为
的左右焦点为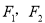 ,
,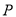 是双曲线右支上一点,满足条件
是双曲线右支上一点,满足条件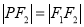 ,直线
,直线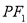 与圆
与圆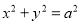 相切,则双曲线的离心率为( )
相切,则双曲线的离心率为( )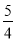 (B)
(B)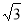 (C)
(C)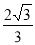 (D)
(D)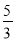
 的图象( )
的图象( ) 轴对称 (B)关于
轴对称 (B)关于 轴对称
轴对称 对称
对称 与圆
与圆 有两个不同交点的一个充分不必要条件是( )
有两个不同交点的一个充分不必要条件是( ) B.
B. C.
C. D.
D.
 ,向量
,向量 ,若
,若 ,则实数
,则实数 的值是( )
的值是( ) B.
B. C.
C. D.
D.