题目内容
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() 底面ABC.M,N分别为PB,PC的中点.
底面ABC.M,N分别为PB,PC的中点.
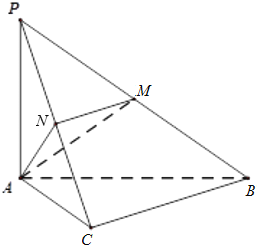
(1)求证:![]() 平面ABC;
平面ABC;
(2)求证:平面![]() 平面PAC;
平面PAC;
(3)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)由题意可得![]() ,再利用线面平行的判定定理即可证出.
,再利用线面平行的判定定理即可证出.
(2)由线面垂直的性质定理可得![]() ,再由
,再由![]() ,利用线面垂直的判定定理可得
,利用线面垂直的判定定理可得![]() 平面PAC,再由面面垂直的判定定理即可证出.
平面PAC,再由面面垂直的判定定理即可证出.
(3)利用等体法:![]()
证明:(1)M,N分别为PB,PC的中点,
所以![]() ,
,![]() 平面ABC,
平面ABC,
![]() 平面ABC,所以
平面ABC,所以![]() 平面ABC;
平面ABC;
(2)![]() 底面ABC,
底面ABC,![]() 平面ABC,所以
平面ABC,所以![]() ,
,
因为![]() ,所以
,所以![]() ,又
,又![]() ,
,
所以![]() 平面PAC,
平面PAC,![]() 平面ABC,所以平面
平面ABC,所以平面![]() 平面PAC;
平面PAC;
(3)由(2)知,![]() ,
,![]() 平面PAC,所以
平面PAC,所以![]() 平面PAC,
平面PAC,
![]() ,
,
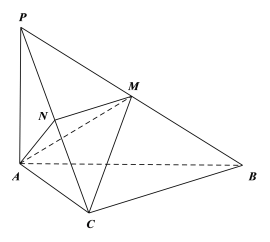
在三角形PAC中,![]() ,
,![]() ,
,
![]() ,
,
所以![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某校初一年级全年级共有![]() 名学生,为了拓展学生的知识面,在放寒假时要求学生在假期期间进行广泛的阅读,开学后老师对全年级学生的阅读量进行了问卷调查,得到了如图所示的频率分布直方图(部分已被损毁),统计人员记得根据频率直方图计算出学生的平均阅读量为
名学生,为了拓展学生的知识面,在放寒假时要求学生在假期期间进行广泛的阅读,开学后老师对全年级学生的阅读量进行了问卷调查,得到了如图所示的频率分布直方图(部分已被损毁),统计人员记得根据频率直方图计算出学生的平均阅读量为![]() 万字.根据阅读量分组按分层抽样的方法从全年级
万字.根据阅读量分组按分层抽样的方法从全年级![]() 人中抽出
人中抽出![]() 人来作进一步调查.
人来作进一步调查.

(1)在阅读量为![]() 万到
万到![]() 万字的同学中有
万字的同学中有![]() 人的成绩优秀,在阅量为
人的成绩优秀,在阅量为![]() 万到
万到![]() 万字的同学中有
万字的同学中有![]() 人成绩不优秀,请完成下面的
人成绩不优秀,请完成下面的![]() 列联表,并判断在“犯错误概率不超过
列联表,并判断在“犯错误概率不超过![]() ”的前提下,能否认为“学生成绩优秀与阅读量有相关关系”;
”的前提下,能否认为“学生成绩优秀与阅读量有相关关系”;
阅读量为 | 阅读量为 | 合计 | |
成绩优秀的人数 | |||
成绩不优秀的人数 | |||
合计 |
(2)在抽出的同学中,1)求抽到被污染部分的同学人数;2)从阅读量在![]() 万到
万到![]() 万字及
万字及![]() 万到
万到![]() 万字的同学中选出
万字的同学中选出![]() 人写出阅读的心得体会.求这
人写出阅读的心得体会.求这![]() 人中恰有
人中恰有![]() 人来自阅读量是
人来自阅读量是![]() 万到
万到![]() 万的概率.
万的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|