题目内容
已知数列 的前
的前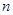 项和为
项和为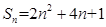 ,数列
,数列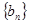 的首项
的首项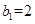 ,且点
,且点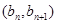 在直线
在直线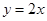 上.
上.
(1)求数列 ,
,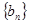 的通项公式;
的通项公式;
(2)若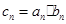 ,求数列
,求数列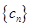 的前
的前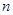 项和
项和 .
.
(1) (2)
(2)
解析试题分析:(1)根据 求出
求出 ,根据已知条件和等比数列定义求出
,根据已知条件和等比数列定义求出 ;(2)应用错项相减法求差比数列的前
;(2)应用错项相减法求差比数列的前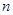 项和.
项和.
试题解析:(1)由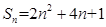 得
得 , 1分
, 1分
∴ 2分
2分
当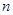 =1时,
=1时, , 3分
, 3分
综上 . 4分
. 4分
∵点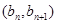 在直线
在直线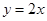 上,∴
上,∴ ,又
,又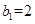 , 5分
, 5分
∴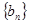 是以2为首项2为公比的等比数列,
是以2为首项2为公比的等比数列, . 7分
. 7分
(2)由(1)知,当 时,
时, ; 8分
; 8分
当 时,
时, , 9分
, 9分
所以当 时,
时, ;
;
当 时,
时, ①
①
则 ② 10分
② 10分
②①得: 12分
12分
即 , 13分
, 13分
显然,当 时,
时, ,
,
所以 . 14分.
. 14分.
考点:等差数列,等比数列的通项求法,差·比数列前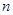 项和求法.
项和求法.

练习册系列答案
相关题目
 前
前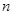 项和
项和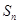 .
.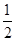 Sn+1(n∈N*);
Sn+1(n∈N*);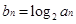 ,cn=
,cn=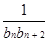 ,且{cn}的前n项和为Tn,求使得
,且{cn}的前n项和为Tn,求使得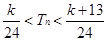 对n∈N*都成立的所有正整数k的值.
对n∈N*都成立的所有正整数k的值. ,满足
,满足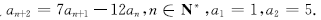
 均为等比数列;
均为等比数列;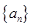 的通项公式
的通项公式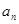 ;
;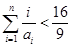 .
.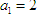 ,点
,点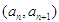 在函数
在函数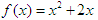 的图象上,其中
的图象上,其中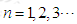
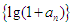 是等比数列,并求数列
是等比数列,并求数列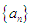 的通项公式;
的通项公式; ,求数列
,求数列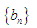 的前
的前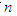 项和
项和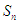 .
. 满足
满足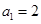 ,
,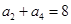 ,且对任意
,且对任意 ,函数
,函数 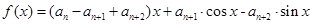 满足
满足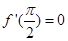
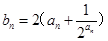 ,求数列
,求数列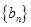 的前
的前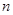 项和
项和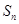 .
.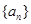 的前
的前 项和为
项和为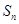 ,且满足
,且满足 .
.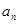 与
与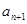 两项之间插入
两项之间插入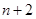 个数构成等差数列,其公差为
个数构成等差数列,其公差为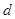 ,求数列
,求数列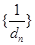 的前
的前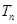 .
. 的各项都是正数,前
的各项都是正数,前 项和是
项和是 ,且点
,且点 在函数
在函数 的图像上.
的图像上. ,求
,求 .
. 的前
的前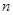 项和为
项和为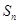 ,且
,且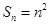 .数列
.数列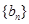 为等比数列,且
为等比数列,且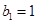 ,
,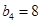 .
. 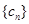 满足
满足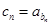 ,求数列
,求数列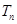 .
.