题目内容
已知数列 的各项都是正数,前
的各项都是正数,前 项和是
项和是 ,且点
,且点 在函数
在函数 的图像上.
的图像上.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求
,求 .
.
(Ⅰ) ;
;
(Ⅱ)  。
。
解析试题分析:(Ⅰ)依题意: 得
得 ,
,
 ,
, 即
即
所以 3分
3分
 所以
所以  6分
6分
(Ⅱ)
 9分
9分
所以  12分
12分
考点:二次函数的图象,数列的通项公式,“裂项相消法”。
点评:中档题,首先根据点在函数的图象上,确定得到 的关系。利用
的关系。利用 的关系求数列的通项公式,往往遵循“两步一验”。“分组求和法”“裂项相消法”“错位相减法”是高考常常考查的数列求和方法。
的关系求数列的通项公式,往往遵循“两步一验”。“分组求和法”“裂项相消法”“错位相减法”是高考常常考查的数列求和方法。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
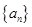 的前
的前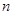 项和为
项和为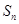 ,且
,且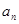 是
是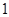 的等差中项,等差数列
的等差中项,等差数列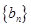 满足
满足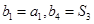
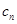 =
=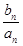 ,求数列
,求数列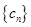 的前
的前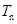 .
. 的前
的前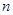 项和为
项和为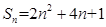 ,数列
,数列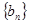 的首项
的首项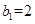 ,且点
,且点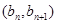 在直线
在直线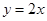 上.
上.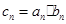 ,求数列
,求数列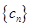 的前
的前 .
. 是函数
是函数 且
且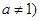 的图像上一点,等比数列
的图像上一点,等比数列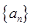 的前
的前 项的和为
项的和为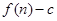 ;数列
;数列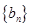
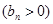 的首项为
的首项为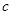 ,且前
,且前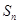 满足
满足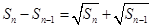
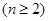 .
.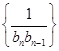 的前
的前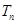 ,问
,问 的最小正整数
的最小正整数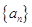 的前n项和为
的前n项和为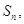 已知
已知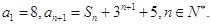
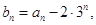 证明:数列
证明:数列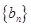 是等比数列;
是等比数列;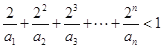 .
. 满足
满足
 ,当
,当 时,求数列
时,求数列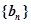 的通项公式.
的通项公式.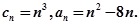 求正整数
求正整数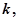 使得一切
使得一切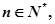 均有
均有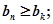
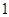
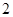
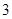
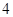
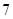
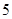
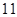
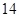
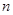 行的第二个数为
行的第二个数为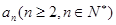 .
.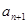 的关系式,并求出
的关系式,并求出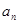 的通项公式.
的通项公式.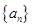 中,
中,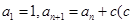 为常数,
为常数, ,且
,且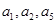 成公比不等于1的等比数列.
成公比不等于1的等比数列.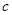 的值;
的值; ,求数列
,求数列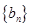 的前
的前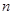 项和
项和 。
。 ,
,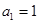 ,前
,前 项和为
项和为 .各项均为正数的等比数列列
.各项均为正数的等比数列列 满足:
满足: ,
, ,且
,且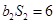 .
.