题目内容

设向量a、b、c满足a+b+c=0，（a-b）⊥c，a⊥b，若|a|=1，则|a|2+|b|2+|c|2的值是_________________.

 

解析：∵a+b+c=0，

∴-c=a+b.

又∵（a-b）⊥c，a⊥b，如图，

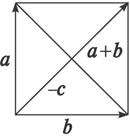
∴可以用向量a、b作出一个正方形.

∵|a|=1，

∴|b|=1，|c|=.

∴|a|2+|b|2+|c|2=4.

答案：4


练习册系列答案
相关题目
设向量
a
，
b，
c
满足
a
+
b
+
c
=
0
，(
a
-
b
)⊥
c
，
a
⊥
b
b，若|
a
|=1，则|
a
|2+|
b
|2+|
c
|2的值是
 
．
设向量
a
、
b
、
c
满足
a
+
b
+
c
=
0
，（
a
-
b
）⊥
c
，
a
⊥
b
，|
a
|=1，则|
c
|=
 
．
设向量
a
，
b
，
c
满足|
a
|=|
b
|=1，
a
•
b
=
1
2
，（ 
a
-
c
）•（ 
b
-
c
）=0，则|
c
|的最大值为（　　）
（2011年高考全国卷理科）设向量
a
、
b
、
c
满足|
a
|=|
b
|=1，
a
•
b
=-
1
2
，＜
a
-
c
，
b
-
c
＞=600，则|
c
|的最大值等于（　　）
设向量
a
，
b
，
c
满足|
a
|=|
b
|=1，
a
•
b
=-
1
2
，＜
a
-
c
，
b
-
c
＞=60°，则|
c
|的最大值等于
2
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网