题目内容
6.不等式组$\left\{\begin{array}{l}y≥0\\ y≥x-2\\ y≤\sqrt{x}\end{array}\right.$所围成的封闭图形的面积为( )| A. | $\frac{10}{3}$ | B. | 2 | C. | 4 | D. | $\frac{17}{5}$ |
分析 由题意画出图象,求出交点坐标,然后利用定积分求封闭图形的面积.
解答 解:由约束条件$\left\{\begin{array}{l}y≥0\\ y≥x-2\\ y≤\sqrt{x}\end{array}\right.$作出可行域如图,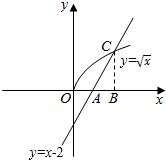
联立$\left\{\begin{array}{l}{y=\sqrt{x}}\\{y=x-2}\end{array}\right.$,解得:C(4,2),
∴不等式组$\left\{\begin{array}{l}y≥0\\ y≥x-2\\ y≤\sqrt{x}\end{array}\right.$所围成的封闭图形的面积为:
S=${∫}_{0}^{4}\sqrt{x}dx{-∫}_{2}^{4}(x-2)dx$=$\frac{2}{3}{x}^{\frac{3}{2}}{|}_{0}^{4}-(\frac{1}{2}{x}^{2}-2x){|}_{2}^{4}$=$\frac{16}{3}-\frac{6}{3}=\frac{10}{3}$.
故选:A.
点评 本题考查基地的线性规划,考查了利用定积分求曲边梯形的面积,体现了数形结合的解题思想方法,是中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
1.下列有关命题的说法正确的是( )
| A. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| B. | 命题“若x=y,则sin x=sin y”的逆否命题为真命题 | |
| C. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| D. | 命题“?x∈R,使得:x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” |