题目内容
点M(5,3)到抛物线y=ax2的准线的距离为6,那么抛物线的方程是( )A.y=12x2
B.y=-36x2
C.y=12x2或y=-36x2
D.y=
 x2或y=-
x2或y=-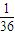 x2
x2
【答案】分析:根据点M到准线的距离为|3+ |=6,分a>0和a<0两种情况分别求得a,进而得到抛物线方程.
|=6,分a>0和a<0两种情况分别求得a,进而得到抛物线方程.
解答:解:当a>0时,开口向上,准线方程为y=- ,则点M到准线的距离为3+
,则点M到准线的距离为3+ =6,求得a=
=6,求得a= ,抛物线方程为y=
,抛物线方程为y= x2,
x2,
当a<0时,开口向上,准线方程为y=- ,点M到准线的距离为|3+
,点M到准线的距离为|3+ |=6解得a=-
|=6解得a=- ,抛物线方程为y=-
,抛物线方程为y=- x2.
x2.
故选D
点评:本题主要考查了抛物线的性质.属基础题.
 |=6,分a>0和a<0两种情况分别求得a,进而得到抛物线方程.
|=6,分a>0和a<0两种情况分别求得a,进而得到抛物线方程.解答:解:当a>0时,开口向上,准线方程为y=-
 ,则点M到准线的距离为3+
,则点M到准线的距离为3+ =6,求得a=
=6,求得a= ,抛物线方程为y=
,抛物线方程为y= x2,
x2,当a<0时,开口向上,准线方程为y=-
 ,点M到准线的距离为|3+
,点M到准线的距离为|3+ |=6解得a=-
|=6解得a=- ,抛物线方程为y=-
,抛物线方程为y=- x2.
x2.故选D
点评:本题主要考查了抛物线的性质.属基础题.

练习册系列答案
相关题目
点M(5,3)到抛物线y=ax2的准线的距离为6,那么抛物线的方程是( )
| A、y=12x2 | ||||
| B、y=-36x2 | ||||
| C、y=12x2或y=-36x2 | ||||
D、y=
|
 x2或y=-
x2或y=- x2
x2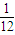 x2或y=-
x2或y=-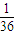 x2
x2