题目内容
已知椭圆C：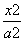
＋
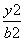＝1(a>b>0)经过点M
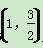，其离心率为
.
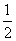(1)求椭圆C的方程；
(2)设直线l：y＝kx＋m(|k|≤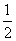)与椭圆C相交于A，B两点，以线段OA，OB为邻边作平行四边形OAPB，其中顶点P在椭圆C上，O为坐标原点．求|OP|的取值范围．
解 (1)由已知，可得e2＝
＝
，所以3a2＝4b2.又点M(1，
)在椭圆C上，所以
＋
＝1.由以上两式联立，解得a2＝4，b2＝3.故椭圆C的方程为
＋
＝1.
(2)当k＝0时，P(0,2m)在椭圆C上，
解得m＝±
，所以|OP|＝
.
当k≠0时，由
消去y并化简整理，得
(3＋4k2)x2＋8kmx＋4m2－12＝0，
Δ＝64k2m2－4(3＋4k2)(4m2－12)＝48(3＋4k2－m2)>0，设A，B，P点的坐标分别为(x1，y1)，(x2，y2)，(x0，y0)，则
综上，所求|OP|的取值范围是
.
练习册系列答案
应用题作业本系列答案
相关题目
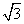)是椭圆上一点，且|PF1|，|F1F2|，|PF2|成等差数列，则椭圆方程为( )
＋
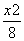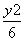＝1 B.
＋
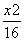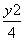＝1 D.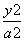
＋
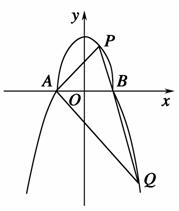
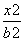＝1(a>b>0，y≥0)和部分抛物线C2：y＝－x2＋1(y≤0)连接而成，C1与C2的公共点为A，B，其中C1的离心率为
.
＋
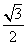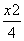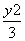＝1的离心率为e，点(1，e)是圆x2＋y2－4x－4y＋4＝0的一条弦的中点，则此弦所在直线的方程是( )
－
＝1与直线x＋y－1＝0相交于P，Q两点，且
＝0(O为原点)，则
－
的值为________．
