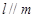题目内容
如图,在四棱锥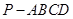 中,
中,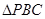 为正三角形,
为正三角形,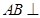 平面
平面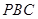 ,
,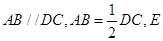 为
为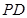 的中点.
的中点.
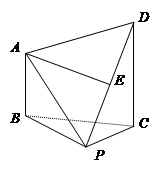
(1)求证: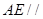 平面
平面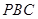 ;
;
(2)求证: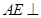 平面
平面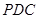 .
.
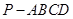 中,
中,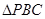 为正三角形,
为正三角形,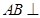 平面
平面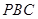 ,
,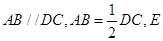 为
为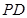 的中点.
的中点.
(1)求证:
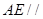 平面
平面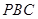 ;
;(2)求证:
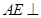 平面
平面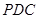 .
.(1)详见解析;(2)详见解析.
试题分析:(1)本题中先取
 的中点
的中点 ,然后根据题意易证
,然后根据题意易证 且
且 ,从而四边形
,从而四边形 是平行四边形,这样就可得到
是平行四边形,这样就可得到 ,最后就是由线面平行的判定定理可得结论;(2)根据(1)中所证得的
,最后就是由线面平行的判定定理可得结论;(2)根据(1)中所证得的 ,要证
,要证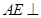 平面
平面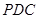 ,只须证
,只须证 平面
平面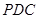 ,由题中的条件不难证明
,由题中的条件不难证明 ,最后由线面垂直的判定定理可得
,最后由线面垂直的判定定理可得 平面
平面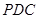 ,根据
,根据 ,可得结论.
,可得结论.试题解析:证明: (1)取
 的中点
的中点 ,连接
,连接

则
 2分
2分
 且
且 ,则四边形
,则四边形 是平行四边形
是平行四边形
 ,
,
 平面
平面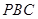 内,所以
内,所以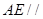 平面
平面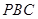 6分
6分(2)

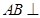 平面
平面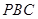 ,
, ,所以
,所以 平面
平面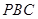 ,而
,而 面
面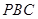 ,所以
,所以
因为
 为
为 的中点且
的中点且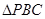 为正三角形,所以
为正三角形,所以
又
 ,所以
,所以 平面
平面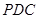
又

 平面
平面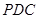 12分.
12分.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
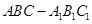 的底面边长是
的底面边长是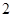 ,侧棱长是
,侧棱长是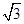 ,
,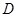 是
是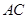 的中点.
的中点.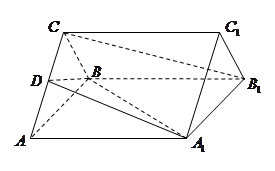
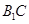 ∥平面
∥平面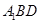 ;
;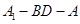 的大小;
的大小;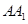 上是否存在一点
上是否存在一点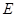 ,使得平面
,使得平面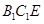
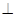 平面
平面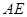 的长;若不存在,说明理由.
的长;若不存在,说明理由.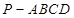 ,
,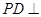 面
面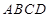 ,
,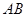 ∥
∥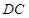 ,
,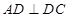 ,
,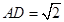 ,
,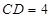 ,
,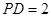 ,
,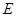 为
为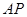 上一点,
上一点,
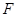 是平面
是平面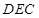 与
与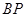 的交点.
的交点.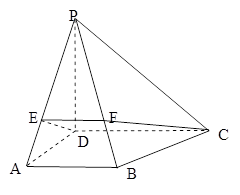
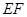 ∥
∥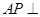 面
面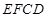 ;
; 与面
与面 中,
中, 平面
平面 ,底面
,底面 ∥
∥ ,
, ,
, ,
,

 ⊥平面
⊥平面 ;
; 与
与 所成角的大小。
所成角的大小。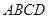 -
-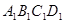 为正方体,下列结论错误的是( )
为正方体,下列结论错误的是( )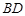 ∥
∥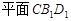
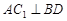
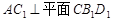
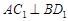
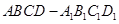 中,下列结论不正确的是 ( )
中,下列结论不正确的是 ( )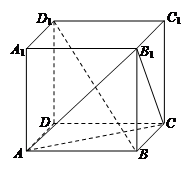
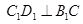
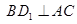
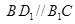
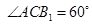
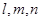 是三条互不相同的空间直线,
是三条互不相同的空间直线,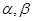 是两个不重合的平面,
是两个不重合的平面,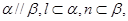 则
则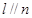 ; ②若
; ②若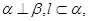 则
则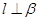 ;
;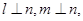 则
则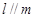 ; ④若
; ④若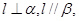 则
则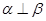
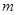 、
、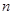 表示不同的直线,
表示不同的直线,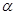 ,
,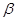 ,
,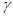 表示不同的平面,则下列四个命题正确的是 .
表示不同的平面,则下列四个命题正确的是 .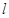 ,且
,且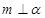 ,则
,则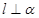 ;②若
;②若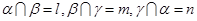 ,则
,则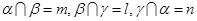 ,且
,且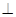 平面
平面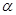 ,直线
,直线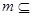 平面
平面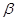 ,则下列四个结论:
,则下列四个结论: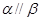 ,则
,则 ②若
②若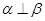 ,则
,则