题目内容
(本题满分15分)已知数列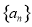 满足
满足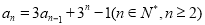 且
且 。
。
(1)求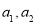 的值;
的值;
(2)是否存在一个实数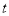 ,使得
,使得 且
且 为等差数列?若存在,求出
为等差数列?若存在,求出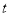 的值;如不存在,请说明理由;
的值;如不存在,请说明理由;
(3)求数列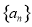 的前n项和
的前n项和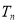 .
.
(1) ,
, ;(2)
;(2) ;(3)
;(3)
【解析】
试题分析:(1)利用递推公式 可得
可得 ,
,
 ,进而
,进而 ;(2)假设
;(2)假设 为等差数列,则
为等差数列,则 应为同一个常数,故
应为同一个常数,故
 应与n无关,所以
应与n无关,所以
 ;(3)由(2)可得
;(3)由(2)可得

 ,利用分足球和及错位相减法可求得
,利用分足球和及错位相减法可求得
试题解析:(1)当n=2时, ,当n=3时,
,当n=3时,
 ,
, . 4分
. 4分
(2)当 时,
时,

 . 7分
. 7分
要使 为等差数列,则必须使
为等差数列,则必须使 , ,
, ,
即存在 ,使
,使 为等差数列. 9分
为等差数列. 9分
(3) 因为当 时,
时, 为等差数列,且
为等差数列,且 ,
,
所以 10分
10分
所以 11分
11分
所以 15分
15分
考点:数列及其综合应用

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
 ,则
,则 的最大值为( )
的最大值为( ) ,则输出的
,则输出的 的最
的最 B.
B. C.
C. D.
D.

 ,
, 是虚数单位,若
是虚数单位,若 与
与 互为共轭复数,则
互为共轭复数,则
 (B)
(B) (C)
(C) (D)
(D)
 ,
, ,若
,若 有两个不相等的实根,则实数
有两个不相等的实根,则实数 的取值范围是
的取值范围是 (B)
(B) (C)
(C) (D)
(D)
 中,
中, ,
, 为
为 中点,点
中点,点 、
、 分别在边
分别在边 、
、 上,且
上,且 ,
, ,若
,若 ,则
,则 = .
= .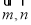 的夹角为
的夹角为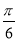 ,且
,且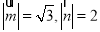 ,在
,在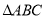 中,
中, ,D为BC的中点,则
,D为BC的中点,则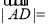 ( )
( )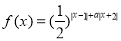 。当
。当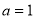 时,
时,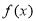 的单调递减区间为 ;
的单调递减区间为 ;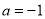 时,
时,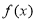 的单调递增区间为 。
的单调递增区间为 。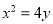 和直线
和直线 所围成的平面图形,绕
所围成的平面图形,绕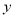 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为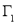 ;由同时满足
;由同时满足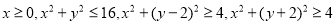 的点
的点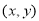 构成的平面图形,绕
构成的平面图形,绕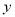 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为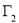 ;根据祖暅原理等知识,通过考察
;根据祖暅原理等知识,通过考察