题目内容
已知G是△ABC的重心,且 ,其中a,b,c分别为角A、B、C的对边,则cosc=
,其中a,b,c分别为角A、B、C的对边,则cosc=
- A.

- B.

- C.

- D.

C
分析:根据G是△ABC的重心则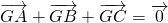 ,而
,而 ,然后根据平面向量基本定理得到a、b、c的等量关系,最后根据余弦定理可得结论.
,然后根据平面向量基本定理得到a、b、c的等量关系,最后根据余弦定理可得结论.
解答:∵G是△ABC的重心
∴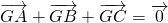
∵
∴a=b= c
c
∴cosC= =
= =
=
故选C.
点评:本题主要考查了向量在几何中的应用,以及重心的性质,同时考查了余弦定理的应用,属于中档题.
分析:根据G是△ABC的重心则
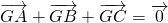 ,而
,而 ,然后根据平面向量基本定理得到a、b、c的等量关系,最后根据余弦定理可得结论.
,然后根据平面向量基本定理得到a、b、c的等量关系,最后根据余弦定理可得结论.解答:∵G是△ABC的重心
∴
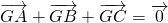
∵

∴a=b=
 c
c∴cosC=
 =
= =
=
故选C.
点评:本题主要考查了向量在几何中的应用,以及重心的性质,同时考查了余弦定理的应用,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
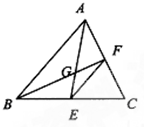 (几何证明选讲选做题)已知G是△ABC的重心,AG交BC于E,BG交AC于F,△EFG的面积为1,则△EFC的面积为
(几何证明选讲选做题)已知G是△ABC的重心,AG交BC于E,BG交AC于F,△EFG的面积为1,则△EFC的面积为