题目内容
设直线
与椭圆
相交于A、B两个不同的点，与x轴相交于点C，记O为坐标原点.
（1）证明：
；
（2）若
的面积取得最大值时的椭圆方程．
（1）见解析
（2）△OAB的面积取得最大值的椭圆方程是
解析:
由 
得
将
代入
消去
得
① ………………………… 3分
由直线l与椭圆相交于两个不同的点得
整理得
，即 ………5分
（2）解：设
由①，得
∵
而点
, ∴
得
代入上式，得
……………8分
于是，△OAB的面积 
--------11分
其中，上式取等号的条件是
即
……………………12分
由可得
将
及
这两组值分别代入①，均可解出
∴△OAB的面积取得最大值的椭圆方程是
练习册系列答案
相关题目
经过点
其离心率为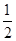
. 
的方程；
与椭圆
为邻边作平行四边形OAPB，其中顶点P在椭圆
为坐标原点.求
的取值范围.
经过点
其离心率为
的方程
与椭圆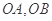
为邻边作平行四边形OAPB，其中顶点P在椭圆
为坐标原点. 求
的距离的最小值.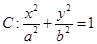
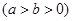经过点
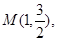其离心率为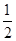
. 
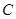的方程；
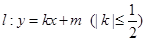与椭圆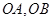
为邻边作平行四边形OAPB，其中顶点P在椭圆
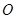为坐标原点.求
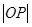的取值范围.
的右焦点为
（3，0），离心率为
。
与椭圆相交于A，B两点，M，N分别为线段
，
的中点，若坐标原点O在以MN为直径的圆上，求
的值。