题目内容
已知椭圆
 经过点
经过点 其离心率为
其离心率为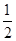 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设直线 与椭圆
与椭圆 相交于A、B两点,以线段
相交于A、B两点,以线段 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆 上,
上, 为坐标原点.求
为坐标原点.求 的取值范围.
的取值范围.
【答案】
(1) (2)
(2) (3)
(3)
【解析】
试题分析:解:(Ⅰ)由已知可得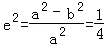 ,所以3a2=4b2①(1分)
,所以3a2=4b2①(1分)
又点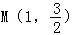 在椭圆C上,
在椭圆C上,
所以 ②(2分)
②(2分)
由①②解之,得a2=4,b2=3.
故椭圆C的方程为 .(5分)
.(5分)
(Ⅱ)当k=0时,P(0,2m)在椭圆C上,解得 ,
,
所以 .(6分)
.(6分)
当k≠0时,则由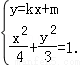
消y化简整理得:(3+4k2)x2+8kmx+4m2﹣12=0,
△=64k2m2﹣4(3+4k2)(4m2﹣12)=48(3+4k2﹣m2)>0③(8分)
设A,B,P点的坐标分别为(x1,y1)、(x2,y2)、(x0,y0),
则 .(9分)
.(9分)
由于点P在椭圆C上,所以 .(10分)
.(10分)
从而 ,化简得4m2=3+4k2,经检验满足③式.(11分)
,化简得4m2=3+4k2,经检验满足③式.(11分)
又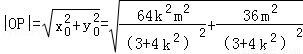
=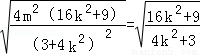
=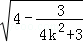 .(12分)
.(12分)
因为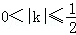 ,得3<4k2+3≤4,有
,得3<4k2+3≤4,有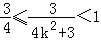 ,
,
故 .(13分)
.(13分)
综上,所求|OP|的取值范围是 .(14分)
.(14分)
考点:直线与圆锥曲线的综合问题
点评:本题主要考查了直线与圆锥曲线的综合问题、椭圆的标准方程问题.当研究椭圆和直线的关系的问题时,常可利用联立方程,进而利用韦达定理来解决

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目

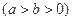 经过点
经过点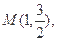 其离心率为
其离心率为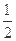
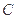 的方程
的方程 与椭圆
与椭圆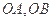 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆 为坐标原点. 求
为坐标原点. 求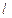 的距离的最小值.
的距离的最小值.
 经过点
经过点 其离心率为
其离心率为
 的方程
的方程 与椭圆
与椭圆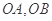 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆 为坐标原点. 求
为坐标原点. 求 的距离的最小值.
的距离的最小值.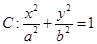
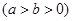 经过点
经过点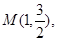 其离心率为
其离心率为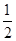 .
. 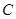 的方程;
的方程;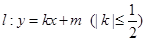 与椭圆
与椭圆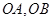 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆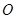 为坐标原点.求
为坐标原点.求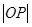 的取值范围.
的取值范围.