Question

【题目】如果函数在定义域内存在区间，使得该函数在区间上的值域为，则称函数是该定义域上的“和谐函数”.

（1）求证：函数是“和谐函数”；

（2）若函数是“和谐函数”，求实数的取值范围.

Answer 1

【答案】（1）见解析；（2）

【解析】试题分析：（1）利用“和谐函数”的定义将问题转化为，再验证进行求解；（2）利用“和谐函数”的定义将问题转化为和的图像至少有2个交点，再利用整体换元和数形结合思想进行求解.

试题解析：（1）要证：存在区间使得在上的值域为，

又由于是一个单调递増的函数，且定义域为

故只需证存在实数满足,且有

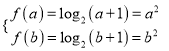
观察得，

即存在符合题意

故函数是“和谐函数”

（2）由题，即存在实数满足，使得在区间上的值域为，

由于单调递増，从而有，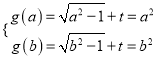

该方程组等价于方程在有至少2个解，

即在上至少有2个解，

即和的图像至少有2个交点，

记，则，从而有，

记，配方得，

又，作出的图像可知， 时有两个交点，

综上， 的取值范围为.