Question

【题目】已知圆过点，且与圆 ()关于轴对称．

(I)求圆的方程；

(II)若有相互垂直的两条直线，都过点，且被圆所截得弦长分别是，求的值.

Answer 1

【答案】(Ⅰ) ；(Ⅱ)28.

【解析】试题分析：

(Ⅰ)由题意可设圆的方程为，结合圆过点计算可得圆的方程.

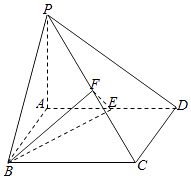
(Ⅱ)解法一：由题意结合几何关系可知四边形为矩形，结合勾股定理计算可得；

解法二：分类讨论：①当一条直线斜率不存在，另一条斜率为0时， 28

②当一条直线斜率存在，结合弦长公式计算可得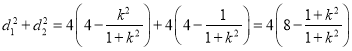=28，即.

试题解析：

（I）由题意设圆的方程

由题意可知圆C的圆心为

则点关于轴对称的点为，∴圆的方程为

将点代入圆的方程得，∴圆的方程

（II）解法一：设被圆所截得弦得中点分别为,

根据圆的性质得四边形为矩形

所以 即 化简得

解法二：①当一条直线斜率不存在，另一条斜率为0时， =28

②当一条直线斜率存在，设为

将点到的距离的平方为，

同理点到的距离的平方为，

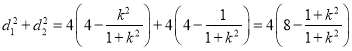=28

由①②可得