题目内容
 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB=| π | 2 |
(1)求证:AD∥平面PCE;
(2)求三棱锥P-ACE的高.
分析:(1)利用线面平行的判定定理证明直线PH∥AD,即可证明AD∥平面PCE.
(2)利用等积法求三棱锥P-ACE的高.
(2)利用等积法求三棱锥P-ACE的高.
解答:(1)设BD∩CE=H,连结PH,
∵P为AB的中点,∴PH为△ABD的中位线,
∴PH∥AD,
∵PH?面PCE,AD?面PCE,
∴AD∥平面PCE.
(2)∵AC=1,AB=3,∠ACB=
,
∴BC=
=
=2
,PC=
AB=
,PA=
,
∴sinA=
=
,
∴△APC的面积为
AC•APsinA=
×1×
×
=
,
∵CD=2,△ABC与矩形BCDE所在的平面互相垂直,
∴三角形ACE为直角三角形,
∴CE=2
.
设三棱锥P-ACE的高为h,
则,VP-ACE=
×
CE?AC?h=
×
×2
h=
h,VE-ACP=
×
×2=
,
∵VE-ACP=VP-ACE
∴等积法得
h=
,解得h=
=
.
即三棱锥P-ACE的高为
.
∵P为AB的中点,∴PH为△ABD的中位线,
∴PH∥AD,
∵PH?面PCE,AD?面PCE,
∴AD∥平面PCE.

(2)∵AC=1,AB=3,∠ACB=
| π |
| 2 |
∴BC=
| 31-1 |
| 8 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴sinA=
| BC |
| AB |
2
| ||
| 3 |
∴△APC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
2
| ||
| 3 |
| ||
| 2 |
∵CD=2,△ABC与矩形BCDE所在的平面互相垂直,
∴三角形ACE为直角三角形,
∴CE=2
| 3 |
设三棱锥P-ACE的高为h,
则,VP-ACE=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 3 |
∵VE-ACP=VP-ACE
∴等积法得
| ||
| 3 |
| ||
| 3 |
| ||
|
| ||
| 3 |
即三棱锥P-ACE的高为
| ||
| 3 |
点评:本题主要考查空间直线和平面平行的判定,利用线面平行的判定定理进行证明即可.求锥体的高,可以考虑使用等积法求解.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
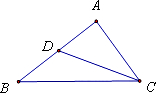 如图所示,在△ABC中,点D是边AB的中点,则向量
如图所示,在△ABC中,点D是边AB的中点,则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
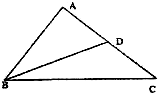 如图所示,在△ABC,已知
如图所示,在△ABC,已知 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD= 如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则
如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=