题目内容
11.解下列方程:(1)8${\;}^{x-1}={2}^{{x}^{2}-1}$;
(2)4•9${\;}^{\frac{1}{x}}$-5•6${\;}^{\frac{1}{x}}$=9•4${\;}^{\frac{1}{x}}$;
(3)5${\;}^{x+3}+{3}^{{x}^{2}+1}=2•{5}^{x+2}+8•{3}^{{x}^{2}}$.
分析 (1)原方程化为:${2}^{3(x-1)}={2}^{{x}^{2}-1}$,可得x2-1=3x-3,解出即可.
(2)原方程化为:$9[(\frac{2}{3})^{\frac{1}{x}}]^{2}$+$5×(\frac{2}{3})^{\frac{1}{x}}$-4=0,解得$(\frac{2}{3})^{\frac{1}{x}}$=$(\frac{2}{3})^{2}$,可得$\frac{1}{x}$=2,解得x并且检验即可得出.
(3)原方程化为:$125×{5}^{x}+3×{3}^{{x}^{2}}$=50×5x+$8×{3}^{{x}^{2}}$,化为$(\frac{3}{5})^{x}$=25,解出即可.
解答 解:(1)原方程化为:${2}^{3(x-1)}={2}^{{x}^{2}-1}$,∴x2-1=3x-3,化为x-3x+2=0,解得x=1,2,∴原方程的解为:x=1,2.
(2)原方程化为:$9[(\frac{2}{3})^{\frac{1}{x}}]^{2}$+$5×(\frac{2}{3})^{\frac{1}{x}}$-4=0,解得$(\frac{2}{3})^{\frac{1}{x}}$=$(\frac{2}{3})^{2}$,∴$\frac{1}{x}$=2,解得x=$\frac{1}{2}$,
经过检验满足原方程,
∴原方程的解为:x=$\frac{1}{2}$.
(3)原方程化为:$125×{5}^{x}+3×{3}^{{x}^{2}}$=50×5x+$8×{3}^{{x}^{2}}$,
化为$(\frac{3}{5})^{x}$=25,
∴x=$lo{g}_{\frac{3}{5}}25$.
原方程的解为:x=$lo{g}_{\frac{3}{5}}25$.
点评 本题考查了指数与对数的运算性质及其方程的解法,考查了推理能力与计算能力,属于中档题.

| A. | y=x2-2x | B. | y=x3 | C. | y=ln$\sqrt{1-{x}^{2}}$ | D. | y=|x|+1 |
| A. | 7 | B. | $\frac{1}{7}$ | C. | -7 | D. | $-\frac{1}{7}$ |
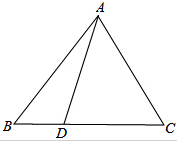 如图,△ABC中,|AB|=|AC|,D是BC边上任意一点,(D与B、C不重合),求证:|AB|2=|AD|2+|BD|•|DC|.
如图,△ABC中,|AB|=|AC|,D是BC边上任意一点,(D与B、C不重合),求证:|AB|2=|AD|2+|BD|•|DC|.