题目内容
13.已知函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+2bx+c,函数f(x)在区间(0,1)内取极大值,在区间(1,2)内取极小值,则u=$\frac{b-2}{a-1}$的取值范围是$(\frac{1}{4},1)$.分析 求出函数的导数,结合二次函数的性质得到关于a,b的不等式组,画出满足条件的平面区域,结合图象求出u的范围即可.
解答 解:f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+2bx+c,
∴f′(x)=x2+ax+2b,
∵函数f(x)在区间(0,1)内取得极大值,在区间(1,2)内取得极小值
∴f′(x)=x2+ax+2b=0在(0,1)和(1,2)内各有一个根
f′(0)>0,f′(1)<0,f′(2)>0
即$\left\{\begin{array}{l}{b>0}\\{a+2b+1<0}\\{a+b+2>0}\end{array}\right.$,
画出满足条件的平面区域,如图示: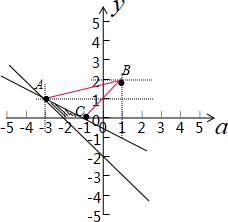 ,
,
由$\left\{\begin{array}{l}{a+2b+1=0}\\{a+b+2=0}\end{array}\right.$,解得:A(-3,1),
则u=$\frac{b-2}{a-1}$的几何意义表示平面区域内的点与(1,2)的直线的斜率,
而KAB=$\frac{1}{4}$,KBC=1,
故u∈$(\frac{1}{4},1)$,
故答案为:$(\frac{1}{4},1)$.
点评 本题考查了函数的单调性问题,考查导数的应用以及简单的线性规划问题,数形结合思想,是一道中档题.

练习册系列答案
相关题目