题目内容
已知双曲线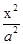
－
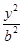＝1(a>0，b>0)的左、右焦点分别为F1(－c,0)、F2(c,0)．若双曲线上存在点P，使
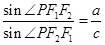，则该双曲线的离心率的取值范围是________．
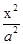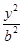－＝1(a>0，b>0)的左、右焦点分别为F1(－c,0)、F2(c,0)．若双曲线上存在点P，使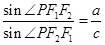，则该双曲线的离心率的取值范围是________．
试题分析：根据正弦定理与题中等式，算出
=e（e是椭圆的离心率）．作出椭圆的左准线l，作PQ⊥l于Q，根据椭圆的第二定义得
＝e，所以|PQ|=|PF2|=
．设P（x，y），将|PF1|、|PF2|表示为关于a、c、e、x的式子，利用|PF2|+|PF1|=2a解出x=
．最后根据椭圆上点的横坐标满足-a≤x≤a，建立关于e的不等式并解之，即可得到该椭圆离心率的取值范围．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
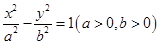的离心率为2,
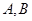为期左右顶点,点P为双曲线C在第一象限的任意一点,点O为坐标原点,若
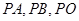的斜率为
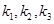,则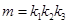
的取值范围为( )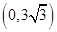
-
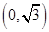
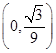
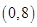
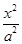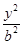=1的离心率为2,焦点与椭圆
+
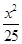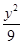=1的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为 .
-
=1(a>0,b>0)与双曲线C2:
-
=1有相同的渐近线,且C1的右焦点为F(
,0),则a= ,b= .
-
=1的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△PQF的周长为 .
，一个焦点到最近顶点的距离是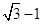
，则双曲线的方程是（ ）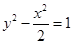
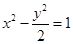
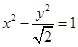
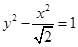
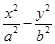＝1(a＞0，b＞0)与双曲线C2：
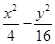＝1有相同的渐近线，且C1的右焦点为F(
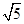，0)，则a＝________，b＝________.
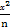-y2=1(n>1)的左、右两个焦点为F1,F2,P在双曲线上,且满足|PF1|+|PF2|=2
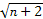,则△PF1F2的面积为( )
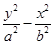＝1(a>0，b>0)，P为x轴上一动点，经过P的直线y＝2x＋m(m≠0)与双曲线C有且只有一个交点，则双曲线C的离心率为________．