题目内容
3.在△ABC中,角A、B、C所对的边分别为a、b、c,且满足c=$\sqrt{3}$,ccosB=(2a-b)cosC.(Ⅰ)求角C的大小;
(Ⅱ)求△ABC的周长的最大值.
分析 (Ⅰ)利用正弦定理结合两角和差的正弦公式进行化简即可求角C的大小;
(Ⅱ)根据余弦定理结合基本不等式的应用求出a+b的范围即可求△ABC的周长的最大值.
解答 解:(Ⅰ)∵ccosB=(2a-b)cosC=2acosC-bcosC,
∴ccosB+bcosC=2acosC,
即sinCcosB+sinBcosC=2sinAcosC,
即sin(B+C)=2sinAcosC,
则sinA=2sinAcosC,
得cosC=$\frac{1}{2}$,即C=$\frac{π}{3}$;
(Ⅱ)∵c2=a2+b2-2abcosCc=$\sqrt{3}$,
∴a2+b2-ab=3,
即(a+b)2=3ab+3,
∵a+b≥2$\sqrt{ab}$,
∴ab≤($\frac{a+b}{2}$)2,
∴(a+b)2=3ab+3≤$\frac{3}{4}$(a+b)2+3,
得(a+b)2≤12,则a+b≤2$\sqrt{3}$,当且仅当a=b=$\sqrt{3}$时取等号,
∴△ABC的周长的最大值是3$\sqrt{3}$.
点评 本题主要考查正弦定理和余弦定理的应用,结合基本不等式的性质是解决本题的关键.综合性较强.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
14.函数y=sinx(cosx-$\sqrt{3}$sinx)(0≤x≤$\frac{π}{2}$)的值域为( )
| A. | [$\sqrt{3}$,1+$\frac{\sqrt{3}}{2}$] | B. | [-$\frac{\sqrt{3}}{2}$,1-$\frac{\sqrt{3}}{2}$] | C. | [0,1] | D. | [-$\sqrt{3}$,1-$\frac{\sqrt{3}}{2}$] |

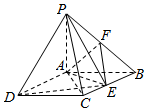 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动. 如图,在△ABC中,∠ABC=90°,AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°.
如图,在△ABC中,∠ABC=90°,AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°.