题目内容
设p：实数x满足x2－4ax＋3a2<0，其中a≠0，q：实数x满足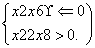
(1)若a＝1，且p∧q为真，求实数x的取值范围；
(2)若p是q的必要不充分条件，求实数a的取值范围．
解：(1)由x2－4ax＋3a2<0，得(x－3a)(x－a)<0，
当a＝1时，解得1<x<3，即p为真时实数x的取值范围是1<x<3.
由
，得2<x≤3，即q为真时实数x的取值范围是2<x≤3.
若p∧q为真，则p真且q真，所以实数x的取值范围是2<x<3.
(2)p是q的必要不充分条件，即q⇒p且p
q，设A＝{x|p(x)}，B＝{x|q(x)}，则A
B，
又B＝(2,3]，当a>0时，A＝(a,3a)；
a<0时，A＝(3a，a)．
所以当a>0时，有
解得1<a≤2；
当a<0时，显然A∩B＝∅，不合题意．
综上所述，实数a的取值范围是1<a≤2.
练习册系列答案
相关题目
上的一点
到椭圆一个焦点的距离为
，则
B 
D 
”的含义为（）
不全为0 
不为0且
为0，或
a＞0”的否定为假命题，则实数a的取值范围是________．
的定义域为集合N，求：
对称．据此可推测，对任意的非零实数a，b，c，m，n，p，关于x的方程m[f(x)]2＋nf(x)＋p＝0的解集都不可能是( )．