题目内容
已知数列{an}的前n项和Sn=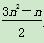 ,n∈N*.
,n∈N*.
(1)求数列{an}的通项公式;
(2)证明:对任意的n>1,都存在m∈N*,使得a1,an,am成等比数列.
解 (1)由Sn=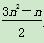 ,得a1=S1=1,
,得a1=S1=1,
当n≥2时,an=Sn-Sn-1=3n-2,
所以数列{an}的通项公式为:an=3n-2.
(2)证明:要使得a1,an,am成等比数列,只需要a =a1·am,即(3n-2)2=1·(3m-2),即m=3n2-4n+2,而此时m∈N*,且m>n.
=a1·am,即(3n-2)2=1·(3m-2),即m=3n2-4n+2,而此时m∈N*,且m>n.
所以对任意的n>1,都存在m∈N*,使得a1,an,am成等比数列.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 |的最小值为________.
|的最小值为________.

 ,则满足an+1<an的n的取值为( )
,则满足an+1<an的n的取值为( )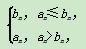 若在数列{cn}中,c5≤cn对任意n∈N*恒成立,则实数k的取值范围是________.
若在数列{cn}中,c5≤cn对任意n∈N*恒成立,则实数k的取值范围是________.