题目内容
设数列{an}的前n项和为Sn.若对任意的正整数n,总存在正整数m,使得Sn=am,则称{an}是“H数列”.
(1)若数列{an}的前n项和Sn=2n(n∈N*),证明:{an}是“H数列”;
(2)设{an}是等差数列,其首项a1=1,公差d<0.若{an}是“H数列”,求d的值;
(3)证明:对任意的等差数列{an},总存在两个“H数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立.
解 (1)首先a1=S1=2,当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1,∴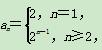
∴对于任意的n∈N*,Sn=2n是数列{an}中的n+1项,因此数列{an}是“H数列”.
(2)由题意an=1+(n-1)d,Sn=n+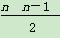 d,数列{an}是“H数列”,则存在k∈N*,使n+
d,数列{an}是“H数列”,则存在k∈N*,使n+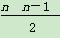 d=1+(k-1)d,k=
d=1+(k-1)d,k=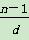 +
+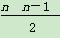 +1,由于
+1,由于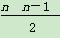 ∈N*,又k∈N*,则
∈N*,又k∈N*,则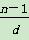 ∈Z对一切正整数n都成立,∴d=-1.
∈Z对一切正整数n都成立,∴d=-1.
(3)若dn=bn(b是常数),则数列{dn}前n项和为Sn=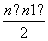 b是数列{dn}中的第
b是数列{dn}中的第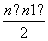 项,因此{dn}是“H数列”,对任意的等差数列{an},an=a1+(n-1)d(d是公差),设bn=na1,cn=(d-a1)(n-1),则an=bn+cn,而数列{bn},{cn}都是“H数列”.
项,因此{dn}是“H数列”,对任意的等差数列{an},an=a1+(n-1)d(d是公差),设bn=na1,cn=(d-a1)(n-1),则an=bn+cn,而数列{bn},{cn}都是“H数列”.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =1,则λ的值为________.
=1,则λ的值为________.
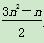 ,n∈N*.
,n∈N*. 图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为公比的数是( )
图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为公比的数是( ) B.
B.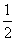
 D.
D.
 则其前6项之和是( )
则其前6项之和是( )