题目内容
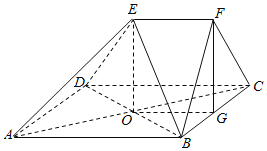
【题目】如图，在多面体ABCDEF中，四边形ABCD是菱形，AC，BD相交于点O，EF∥AB，EF
AB，平面BCF⊥平面ABCD，BF＝CF，G为BC的中点，求证：
（1）OG∥平面ABFE；
（2）AC⊥平面BDE．
【答案】（1）见解析（2）见解析
【解析】
（1）根据中位线的性质证明OG∥AB后即可得证；
（2）连接FG、EO，由题意EO⊥平面ABCD，可得EO⊥AC，由线面垂直的判定即可得解.
证明：（1）∵四边形ABCD是菱形，AC，BD相交于点O，
∴O是AC中点，
∵G为BC的中点，∴OG∥AB，
∵OG平面ABFE，AB平面ABFE，
∴OG∥平面ABFE．
（2）连接FG、EO，
∵四边形ABCD是菱形，AC，BD相交于点O，
∴AC⊥BD，O是AC中点，
∵G为BC的中点，∵EF∥AB，EF
AB，平面BCF⊥平面ABCD，BF＝CF，
∴FG⊥平面ABCD，∴EO⊥平面ABCD，∴EO⊥AC，
∵EO∩BD＝O，∴AC⊥平面BDE．
【题目】网购已经成为一种新型的购物方式，2018年天猫双11，仅1小时47分钟成交额超过1000亿元，比2017年达到1000亿元的时间缩短了7个小时，为了研究市民对网购的依赖性，从A城市16﹣59岁人群中抽取一个容量为100的样本，得出下列2×2列联表，其中16﹣39岁为青年，40﹣59岁为中年，当日消费金额超过1000元为消费依赖网购，否则为消费不依赖网购．
依赖网购 | 不依赖网购 | 小计 | |
青年（16﹣39岁） | 40 | 20 | |
中年（40﹣59岁） | 20 | 20 | |
小计 |
（1）完成2×2列联表，计算X2值，并判断是否有95%的把握认为网购依赖和年龄有关？
（2）把样本中的频率当作概率，随机从A城市中选取5人，其中依赖网购的人数为随机变量X，求随机变量X的分布列及期望（附：X2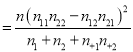
，当X2＞3.841时，有95%的把握说事件A与B有关，当X2≤3.841时，没有95%的把握说事件A与B有关）
