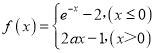题目内容
【题目】某企业要设计制造一批大小、规格相同的长方体封闭水箱,已知每个水箱的表面积为432(每个水箱的进出口所占面积与制作材料的厚度均忽略不计).每个长方体水箱的底面长是宽的2倍.现设每个长方体水箱的底面宽是![]() ,用
,用![]() 表示每个长方体水箱的容积.
表示每个长方体水箱的容积.
(1)试求函数![]() 的解析式及其定义域;
的解析式及其定义域;
(2)当![]() 为何值时,
为何值时,![]() 有最大值,并求出最大值.
有最大值,并求出最大值.
【答案】(1)![]() ,定义域为
,定义域为![]() ;(2)当
;(2)当![]() 时,
时,![]() 有最大值,为576.
有最大值,为576.
【解析】
(1)由题意得长方体的高![]()
![]() ,根据长方体的体积公式可得
,根据长方体的体积公式可得![]() ,然后根据实际情况得到定义域.(2)利用导数判断出函数
,然后根据实际情况得到定义域.(2)利用导数判断出函数![]() 的单调性,进而可得最值.
的单调性,进而可得最值.
(1)依题意,每个长方体水箱的底面宽是![]() ,则长是
,则长是![]() ,设其高为
,设其高为![]() ,
,
所以其表面积为![]() ,
,
解得![]()
![]() ,
,
所以![]() ,
,
由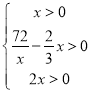 ,解得
,解得![]() ,
,
所以函数![]() 的定义域为
的定义域为![]() .
.
(2)由(1)知![]()
![]() ,
,
所以![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
从而![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
故当![]() 时,
时,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目