题目内容
12.设A={(x,y)|y=1+$\sqrt{4-{x}^{2}}$},B={(x,y)|y=k(x-2)+4},若A∩B中含有两个元素,则实数k的取值范围是($\frac{5}{12}$,$\frac{3}{4}$].分析 集合A表示圆心为(0,1),半径为2的上半圆;集合B表示恒过(2,4)的直线,要使两集合交集有两个元素,得到两函数图象有两个交点,根据图形确定出k的范围即可.
解答  解:集合A中y=1+$\sqrt{4-{x}^{2}}$,
解:集合A中y=1+$\sqrt{4-{x}^{2}}$,
变形得:x2+(y-1)2=4(y≥1),
表示圆心为(0,1),半径为2的上半圆;
集合B中y=k(x-2)+4=kx-2k+4,表示恒过(2,4)的直线,
由A∩B中含有两个元素,得到两函数图象有两个交点,
当直线与圆相切时,圆心到直线的距离d=r,即$\frac{|-2k+3|}{\sqrt{{k}^{2}+1}}$=2,
解得:k=$\frac{5}{12}$,
当直线过点B(-2,1)时,把B坐标代入直线方程得:1=-2k-2k+4,
解得:k=$\frac{3}{4}$,
则实数k的取值范围为($\frac{5}{12}$,$\frac{3}{4}$].
故答案为:($\frac{5}{12}$,$\frac{3}{4}$]
点评 此题考查了交集及其运算,利用了数形结合的思想,画出正确的图形是解本题的关键.

练习册系列答案
相关题目
3.设全集$U=\left\{{({x,y})\left|{y=x+1,x,y∈R}\right.}\right\},M=\left\{{({x,y})\left|{\frac{y-3}{x-2}=1}\right.}\right\}$,则∁UM=( )
| A. | ∅ | B. | {(2,3)} | C. | (2,3) | D. | {2,3} |
4.f(x)是偶函数且在[0,+∞)上是减函数,且f(log2x)>f(1),则x的取值范围是( )
| A. | ($\frac{1}{2}$,1) | B. | (0,$\frac{1}{2}$)∪(1,+∞) | C. | ($\frac{1}{2}$,2) | D. | (0,1)∪(2,+∞) |
1.设A={x∈R|$\frac{1}{x}$≥1},B={x∈R|ln(1-x)≤0},则“x∈A”是“x∈B”的( )
| A. | 充分不必要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充要条件 | D. | 必要不充分条件 |
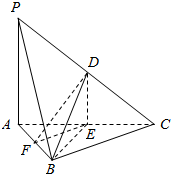 如图所示,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.
如图所示,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.