Question

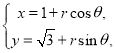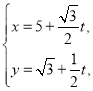【题目】在平面直角坐标系中，曲线：（为参数，），曲线：（为参数）.若曲线和相切.

（1）在以为极点，轴非负半轴为极轴的极坐标系中，求曲线的极坐标方程；

（2）若点，为曲线上两动点，且满足，求面积的最大值.

Answer 1

【答案】(1) ;(2)

【解析】

（1）消去参数，将圆的参数方程，转化为普通方程，再由圆心到直线的距离等于半径，可求得圆的普通方程，最后利用求得圆的极坐标方程.

（2）利用圆的参数方程以及辅助角公式，由此求得的面积的表达式，再由三角函数最值的求法，求得三角形面积的最大值.

解：（1）曲线的参数方程为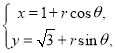（为参数，），

所以其普通方程为，曲线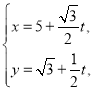：（为参数），所以其普通方程为，若曲线和相切，则，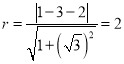

所以曲线的极坐标方程为.

（2）设，所以所以当时，面积的最大值为.