题目内容
11.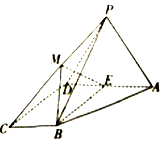 如图,四棱锥P-ABCD的底面为直角梯形,AD∥BC,AD=2BC=2,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为正三角形,M是棱PC上的一点(异于端点).
如图,四棱锥P-ABCD的底面为直角梯形,AD∥BC,AD=2BC=2,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为正三角形,M是棱PC上的一点(异于端点).(Ⅰ)若M为PC中点,求证:PA∥平面BME;
(Ⅱ)是否存在点M,使二面角M-BE-D的大小为30°.若存在,求出点M的位置;若不存在,说明理由.
分析 (Ⅰ)连接AC交BE与点F,连接CE,推导出四边形ABCE为平行四边形,从而MF∥PA,由此能证明PA∥平面BME.
(Ⅱ)连接PE,以E为坐标原点建立如图所示空间直角坐标系,利用向量法能求出存在点M满足条件,且M为棱PC上靠近端点C的四等分点.
解答 证明:(Ⅰ)如图,连接AC交BE与点F,连接CE,
由题意知BC∥AE且BC=AE,故四边形ABCE为平行四边形,
∴F为AC中点,
∴在△PAC中,又由M为PC中点有:MF∥PA,
又MF⊆面BME,PA?面BME,
∴PA∥平面BME.
解:(Ⅱ)连接PE,则由题意知PE⊥平面ABCD,
故以E为坐标原点建立如图所示空间直角坐标系,
则$E({0,0,0}),P({0,0,\sqrt{3}}),B({\sqrt{3},0,0}),C({\sqrt{3},-1,0})$,
设$\overrightarrow{PM}=λ\overrightarrow{PC}=({0<λ<1})$,则$M({\sqrt{3}λ,-λ,({1-λ})\sqrt{3}})$,
∴$\overrightarrow{EM}=({\sqrt{3}λ,-λ,({1-λ})\sqrt{3}}),\overrightarrow{EB}=({\sqrt{3},0,0})$,
记平面DBE的法向量$\overrightarrow{n}$=(0,0,1),平面BME的法向量$\overrightarrow{m}$=(x,y,z),
则由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{EM}=\sqrt{3}λx-λy+(1-λ)\sqrt{3}z=0}\\{\overrightarrow{m}•\overrightarrow{EB}=\sqrt{3}x=0}\end{array}\right.$,有$\left\{\begin{array}{l}\sqrt{3}λx-λy+({1-λ})\sqrt{3}z=0\\ \sqrt{3}x=0\end{array}\right.$
令$y=\sqrt{3}$,得$\overrightarrow{m}$=(0,$\sqrt{3}$,$\frac{λ}{1-λ}$),
又由二面角M-BE-D的大小为30°,得$\frac{|\overrightarrow{n}•\overrightarrow{m}|}{|\overrightarrow{n}|•|\overrightarrow{m}|}$=$\frac{|\frac{λ}{1-λ}|}{\sqrt{3+(\frac{λ}{1-λ})^{2}}}$=cos30°=$\frac{\sqrt{3}}{2}$,
解得$λ=\frac{3}{4}$,∴$M=({\frac{{3\sqrt{3}}}{4},-\frac{3}{4},\frac{{\sqrt{3}}}{4}})$
故存在点M满足,且M为棱PC上靠近端点C的四等分点.
点评 本题考查线面平行的证明,考查满足条件的点是否存在的判断与求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | 43个 | B. | 45个 | C. | 46个 | D. | 48个 |
| A. | -2 | B. | -1 | C. | $\frac{3}{2}$ | D. | 2 |