Question

已知椭圆C的焦点F₁（－，0）和F₂（，0），长轴长6。

(1)设直线交椭圆C于A、B两点，求线段AB的中点坐标。

(2) 求过点(0，2)的直线被椭圆C所截弦的中点的轨迹方程

Answer 1

解:由已知条件得椭圆的焦点在x轴上,其中c=,a=3,从而b=1,所以其标准方程是:

.联立方程组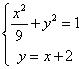,消去y得, .

设A(),B(),AB线段中点为M()那么: ,

所以

也就是说线段AB中点坐标为

（2）设直线方程为y＝kx＋2，

把它代入x²＋9y²＝9

整理得  (9k²＋1)x²＋36kx＋27＝0

要使直线和椭圆有两个不同交点，则Δ＞0，即

k＜－，

设直线与椭圆两个交点为A(x₁，y₁)，B(x₂，y₂)，中点坐标为C(x，y)，则

x＝

y＝

从参数方程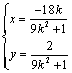 (k＜－)

消去k得  x²＋9(y－1)²＝9

且｜x｜＜，0＜y＜．

综上，所求轨迹方程为，其中，