向量$\overrightarrow a.\overrightarrow b.\overrightarrow c$满足$|{\overrightarrow a}|=|{\overrightarrow b}|=1.\overrightarrow a•\overrightarrow b=-\frac{1}{2}.\left?{\overrightarrow a-\overrightarr 题目和参考答案——青夏教育精英家教网——

题目内容

19．向量$\overrightarrow a，\overrightarrow b，\overrightarrow c$满足$|{\overrightarrow a}|=|{\overrightarrow b}|=1，\overrightarrow a•\overrightarrow b=-\frac{1}{2}，\left?{\overrightarrow a-\overrightarrow c，\overrightarrow b-\overrightarrow c}\right＞={60^0}$，则$\overrightarrow c$的模长的最大值为（　　）

A．

2

B．

$\sqrt{3}$

C．

$\sqrt{2}$

D．

1

分析计算$\overrightarrow{a}，\overrightarrow{b}$的夹角，得出$\overrightarrow{a}，\overrightarrow{b}，\overrightarrow{c}$的起点和终点共圆，则外接圆的直径即为|$\overrightarrow{c}$|的最大值．

解答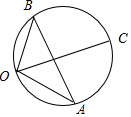解：设$\overrightarrow{OA}=\overrightarrow{a}$，$\overrightarrow{OB}=\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，
则OA=OB=1，
∵$\overrightarrow{a}•\overrightarrow{b}$=1×1×cos∠AOB=-$\frac{1}{2}$，∴∠AOB=120°，
∵＜$\overrightarrow{a}-\overrightarrow{c}$，$\overrightarrow{b}-\overrightarrow{c}$＞=∠BCA=60°，
∴O，A，B，C四点共圆，
设△AOB的外接圆半径为r，则2r=$\frac{OA}{sin∠OBA}$=2，
∴OC的最大值为2r=2．
故选：A．

点评本题考查了平面向量的基本定理，属于中档题．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

9．已知曲线C的极坐标方程为ρ²-2$\sqrt{2}$ρcos（θ+$\frac{π}{4}$）-2=0，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系xOy．
（1）若直线l过原点，且被曲线C截得的弦长最小，求直线l的直角坐标方程；
（2）若M是曲线C上的动点，且点M的直角坐标为（x，y），求x+y的最大值．

10．已知向量$|{\overrightarrow a}|=1，|{\overrightarrow b}|=2$．
（Ⅰ）若$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$，求$|{\overrightarrow a+2\overrightarrow b}|$；
（Ⅱ）若$（2\overrightarrow a-\overrightarrow b）•（3\overrightarrow a+\overrightarrow b）=3$，求$\overrightarrow a$与$\overrightarrow b$的夹角．

7．复数$\frac{1}{i-2}$的虚部为（　　）

$-\frac{1}{5}i$

14．已知函数f（x）=x²-ax（a≠0），g（x）=lnx，f（x）的图象在它与x轴异于原点的交点M处的切线为l₁，g（x-1）的图象在它与x轴的交点N处的切线为l₂，且l₁与l₂平行．
（1）求a的值；
（2）已知t∈R，求函数y=f（xg（x）+t）在x∈[1，e]上的最小值h（t）；
（3）令F（x）=g（x）+g′（x），给定x₁，x₂∈（1，+∞），x₁＜x₂，对于两个大于1的正数α，β，存在实数m满足：α=mx₁+（1-m）x₂，β=（1-m）x₁+mx₂，并且使得不等式|F（α）-F（β）|＜|F（x₁）-F（x₂）|恒成立，求实数m的取值范围．．

4．过双曲线的一个焦点F₂作垂直于实轴的弦PQ，F₁是另一焦点，若△PF₁Q是等腰直角三角形，则双曲线的离心率e等于（　　）

如图，在五面体ABCDEF中，AB∥CD∥EF，CD=EF=CF=2AB=2AD=2，∠ACF=60°，AD⊥CD，平面CDEF⊥平面ABCD，P是BC的中点，
（1）求异面直线BE与PF所成角的余弦值；
（2）在直线EF上，是否存在一点Q，使得PQ∥平面EBD，若存在，求出该点；若不存在请说明理由．

8．已知椭圆$\frac{y^2}{4}+\frac{x^2}{3}=1$与抛物线y=ax²（a＞0）有相同的焦点，则抛物线的焦点到准线的距离为2．

9．从1，2，3，4这4个数中，任取两个数，两个数都是奇数的概率是（　　）