题目内容
设x>2y>0,平面向暈
=(x,
),
=(x,
+
),则
•
的最小值是( )
| m |
| 1 |
| x |
| n |
| 1 |
| 2y |
| 1 |
| x-2y |
| m |
| n |
| A、1 | B、4 | C、3 | D、2 |
分析:利用两个向量的数量积公式化简
•
的解析式,并使用基本不等式可求得
•
的最小值.
| m |
| n |
| m |
| n |
解答:解:∵x>2y>0,
∵
•
=(x,
)•(x,
+
)=x2+
+
=x2 +
+
=( x2-2xy)+2xy+
+
≥4
=4,
当且仅当(x2-2xy)=2xy=
=
时,等号成立,故
•
的最小值是 4,
故选B.
∵
| m |
| n |
| 1 |
| x |
| 1 |
| 2y |
| 1 |
| x-2y |
| 1 |
| 2xy |
| 1 |
| x(x-2y) |
| 1 |
| 2xy |
| 1 |
| x(x-2y) |
| 1 |
| 2xy |
| 1 |
| 2y(x-2y) |
( x2-2xy) • 2xy •
|
当且仅当(x2-2xy)=2xy=
| 1 |
| 2xy |
| 1 |
| x(x-2y) |
| m |
| n |
故选B.
点评:本题考查两个向量的数量积公式的应用,以及基本不等式的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设二元一次不等式组
所表示的平面区域为M.若曲线x2-my2=1总经过区域M,则实数m的取值范围是( )
|
A、(-∞,
| ||
| B、[15,+∞) | ||
C、(
| ||
D、[
|
 =(x,
=(x, ),
), =(x,
=(x,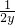 +
+ ),则
),则