题目内容
16.在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AB⊥BC侧面PAB⊥底面ABCD,PA=AD=AB=2,BC=4.
(1)若PB中点为E.求证:AE∥平面PCD;
(2)若∠PAB=60°,求直线BD与平面PCD所成角的正弦值.
分析 (1)取PC中点F,并连接DF,FE,根据已知条件容易说明四边形ADFE为平行四边形,从而有AE∥DF,根据线面平行的判定定理即得到AE∥平面PCD;
(2)设B到平面PCD的距离为h,从而直线BD与平面PCD所成角的正弦值便可表示为$\frac{h}{BD}$,BD根据已知条件容易求出,而求h可通过VP-BCD=VB-PCD求出:取AB中点O,连接PO,可以说明PO⊥平面ABCD,而根据已知条件能够求出S△BCD,S△PCD,从而求出h,从而求得答案.
解答 解:(1)证明:如图,取PC的中点F,连结DF,EF;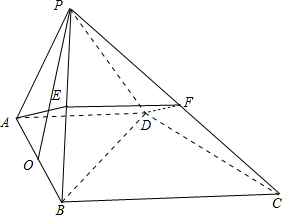 ∵EF∥AD,且AD=EF,所以ADFE为平行四边形;
∵EF∥AD,且AD=EF,所以ADFE为平行四边形;
∴AE∥DF,且AE?平面PCD,DF?平面PCD;
∴AE∥平面PCD;
(2)
∵∠PAB=60°,PA=AB;
∴△PAB为等边三角形,取AB中点O,连接PO;
则PO⊥AB;
又侧面PAB⊥底面ABCD,平面PAB∩平面ABCD=AB;
∴PO⊥平面ABCD;
根据已知条件可求得PO=$\sqrt{3}$,S△BCD=4,PD=CD=$2\sqrt{2}$,PC=2$\sqrt{5}$,${S}_{△PCD}=\sqrt{15}$;
设点B到平面PCD的距离为h;
∴${V_{P-BCD}}=\frac{4}{3}\sqrt{3}$,${V}_{B-PCD}=\frac{\sqrt{15}}{3}h$;
∵VP-BCD=VB-PCD;
∴$h=\frac{4}{\sqrt{5}}$;
∴直线BD与平面PCD所成角θ的正弦值$sinθ=\frac{h}{BD}=\frac{{\frac{4}{{\sqrt{5}}}}}{{2\sqrt{2}}}=\frac{{\sqrt{10}}}{5}$.
点评 考查中位线的性质,平行四边形的定义,线面平行的判定定理,以及直角三角形边的关系,面面垂直的性质定理,棱锥的体积公式,线面角的定义.

 学习实践园地系列答案
学习实践园地系列答案| 所取球的情况 | 三个球均为红色 | 三个球均不同色 | 恰有两球为红色 | 其他情况 |
| 所获得的积分 | 180 | 90 | 60 | 0 |
(Ⅱ)设一次摸奖中,他们所获得的积分为X,求X的分布列及均值(数学期望)E(X);
(Ⅲ)按照以上规则重复摸奖三次,求至少有两次获得积分为60的概率.
| A. | y=±$\frac{1}{2}$x | B. | y=±2x | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |