题目内容
4.在?ABCD中,AB=4$\sqrt{6}$cm,AD=4$\sqrt{3}$cm,∠A=45°,求这个四边形两条对角线的长度和平行四边形的面积.分析 根据余弦定理即可求出四边形两条对角线的长度,再根据平行四边形的面积公式计算即可.
解答 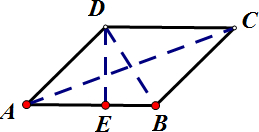 解:连接AC,BD,过点D做DE⊥AB,垂足为E,如图所示,
解:连接AC,BD,过点D做DE⊥AB,垂足为E,如图所示,
∵四边形ABCD为平行四边形,∠A=45°,
∴∠B=135°,BC=AD=AD=4$\sqrt{3}$cm,
根据余弦定理,得
(BD)2=(AD)2+(AB)2-2AD•ABcosA,(AC)2=(BC)2+(AB)2-2BC•ABcosB,
∴(BD)2=(4$\sqrt{3}$)2+(4$\sqrt{6}$)2-2×$4\sqrt{3}$×4$\sqrt{6}$cos45°=(4$\sqrt{3}$)2,(AC)2=(4$\sqrt{3}$)2+(4$\sqrt{6}$)2-2×$4\sqrt{3}$×4$\sqrt{6}$cos135°=16×15,
∴BD=4$\sqrt{3}$,AC=4$\sqrt{15}$,
在Rt△DEA中,DE=ADsinA=4$\sqrt{3}$×$\frac{\sqrt{2}}{2}$=2$\sqrt{6}$cm,
∴SABCD=AB•DE=4$\sqrt{6}$×2$\sqrt{6}$=48cm2,
(或者SABCD=2S△ABD=2×$\frac{1}{2}$AB•AD•ADsinA=48cm2).
点评 本题考查了余弦定理和三角形的面积公式,属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
10. 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了若干名学生的体检表,并得到如图直方图:
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了若干名学生的体检表,并得到如图直方图:
(Ⅰ)若直方图中前三组的频率成等比数列,后四组的频率成等差数列,试估计全年级视力在5.0以下的人数;
(Ⅱ)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?附:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了若干名学生的体检表,并得到如图直方图:
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了若干名学生的体检表,并得到如图直方图:(Ⅰ)若直方图中前三组的频率成等比数列,后四组的频率成等差数列,试估计全年级视力在5.0以下的人数;
(Ⅱ)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
12.己知正四棱锥S-ABCD的侧棱长与底面边长都相等,E是SB的中点,则AE,SD所成角的余弦值为( )
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2}{3}$ |
13.函数f(x)=$\left\{\begin{array}{l}{\sqrt{x}-1,x≥0}\\{2cosx-1,-2π≤x<0}\end{array}\right.$的所有零点的和等于( )
| A. | 1-2π | B. | 1-$\frac{3π}{2}$ | C. | 1-π | D. | 1-$\frac{π}{2}$ |

 如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的表面积为8+12$\sqrt{2}$.
如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的表面积为8+12$\sqrt{2}$.