题目内容
求f(x)=x+
(b>0)的单调区间.
| b |
| x |
考点:函数的单调性及单调区间
专题:函数的性质及应用
分析:先求出函数的定义域,再利用求导公式求出函数的导数,由y′>0和y′<0分别解出函数的递增区间和递减区间.
解答:
解:∵y=x+
(b>0),x≠0,
∴y′=1-
=
,
令y′>0,解得x>
或x<-
;
令y′<0,解得-
<x<0或0<x<
;
故y=x+
(a>0)在(-∞,-
],(
,+∞)上是增函数,在(0,
],(-
,0)上是减函数.
| b |
| x |
∴y′=1-
| b |
| x2 |
| x2-b |
| x2 |
令y′>0,解得x>
| b |
| b |
令y′<0,解得-
| b |
| b |
故y=x+
| b |
| x |
| b |
| b |
| b |
| b |
点评:本题综合考查了利用导数求函数的单调性和不等式的解法,注意定义域要优先考虑.

练习册系列答案
相关题目
设变量x,y满足|x-1|+|y-a|≤1,若2x+y的最大值是5,则实数a的值是( )
| A、2 | B、1 | C、0 | D、-1 |
定义表示不超过x的最大整数[x],记{x}=x-[x],二次函数y=-x2+mx-2与函数y={-x}在(-1,0]上有两个不同的交点,则m的取值范围是( )
A、(-
| ||||
B、(
| ||||
| C、∅ | ||||
| D、以上均不正确 |
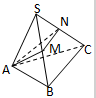 如图,△ABC外一点S,且SA⊥平面ABC,∠ABC=90°,AM⊥SB,AN⊥SC
如图,△ABC外一点S,且SA⊥平面ABC,∠ABC=90°,AM⊥SB,AN⊥SC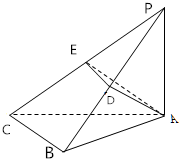 如图,PA⊥平面ABC,AB⊥BC,AD⊥PB,AE⊥PC,AP=
如图,PA⊥平面ABC,AB⊥BC,AD⊥PB,AE⊥PC,AP=