题目内容
若sin(α-β)sinβ-cos(α-β)cosβ=| 1 | 3 |
分析:观察已知条件可知,符合两角差的余弦,从而可得cosα,结合α是第三象限角及同角平方关系可求答案.
解答:解:∵sin(α-β)sinβ-cos(α-β)cosβ=
,
∴cos(α-β+β)=-
,即cosα=-
,
∵α是第三象限角∴sinα=-
故答案为:-
| 1 |
| 3 |
∴cos(α-β+β)=-
| 1 |
| 3 |
| 1 |
| 3 |
∵α是第三象限角∴sinα=-
2
| ||
| 3 |
故答案为:-
2
| ||
| 3 |
点评:本题主要考查了两角和的余弦公式,同角平方关系的简单运用,属于基础试题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
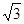 ,且c =
,且c =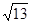 ,C =
,C =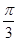 ,求a,b的值
,求a,b的值