题目内容
3.圆锥的高为1,底面半径也为1,过圆锥顶点的截面中,最大的截面面积是1.分析 作出直观图,设OC=a,用a表示出截面△SAB的面积,根据a的范围求出截面的最大值.
解答 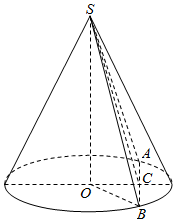 解:设截面SAB与底面交于AB,过底面中心O作OC⊥AB,垂足为C,连结SC,OB.则SO=OB=1.
解:设截面SAB与底面交于AB,过底面中心O作OC⊥AB,垂足为C,连结SC,OB.则SO=OB=1.
设OC=a,则BC=$\sqrt{O{B}^{2}-O{C}^{2}}=\sqrt{1-{a}^{2}}$.SC=$\sqrt{S{O}^{2}+O{C}^{2}}$=$\sqrt{1+{a}^{2}}$.0≤a<1.
∴S△SAB=$\frac{1}{2}AB×SC$=$\sqrt{1-{a}^{2}}×\sqrt{1+{a}^{2}}$=$\sqrt{1-{a}^{4}}$.
∴当a=0时,S△SAB取得最大值1.
故答案为:1.
点评 本题考查了圆锥的结构特征,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
11.已知$tan(x+\frac{π}{4})=2$,则sin2x=( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |