题目内容
AB是过抛物线y2=2px(p>0)焦点F的一条弦,且|AF|=1,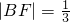 ,求抛物线及直线AB方程.
,求抛物线及直线AB方程.
解:设A(x1,y1),B(x2,y2),
则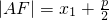 ,
,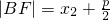 ,…(2分)
,…(2分)
则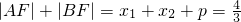 ,
,
∴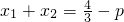 ,…(4分)
,…(4分)
而若设过焦点( ,0)的直线斜率存在且不为0,则可设AB的方程为:y=k(x-
,0)的直线斜率存在且不为0,则可设AB的方程为:y=k(x- )
)
又因为A,B两点是直线AB与抛物线的交点,则
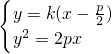 ,?x2-(
,?x2-( +p)x+
+p)x+ =0
=0
∴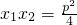 ,
,
由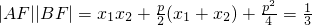 .
.
得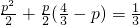 ,…(6分)
,…(6分)
即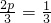 ,
,
∴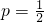 ,
,
抛物线方程为y2=x.…(8分)
设直线AB的倾斜角为θ,
又根据两点间的距离公式得:|AB|2=(y2-y1)2+(x2-x1)2=(tan2θ+1)(x2-x1)2
由于直线AB过点( ,0),设直线AB为y=tanθ(x-
,0),设直线AB为y=tanθ(x- ),
),
联立得到:tan2θx2-(tan2θ+2)px+ p2tan2θ=0
p2tan2θ=0
那么(x2-x1)2
=(x2+x1)2-4x1x 2
=(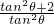 ×p)2-4×
×p)2-4×
=4p2(tan2θ+1)×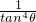
那么|AB|2=(tan2θ+1)(x2-x1)2
=(tan2θ+1)×4p2(tan2θ+1)×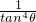
=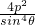 .
.
∴ ,
,
由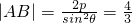 ,得
,得 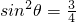 ,
,
∴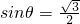 ,∴θ=600或1200,
,∴θ=600或1200,
得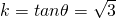 ,
,
所以AB方程为 .…(12分)
.…(12分)
分析:设出A,B两点的坐标,根据抛物线定义可分别表示出|AF|和|BF|,进而可求得|AF|+|BF|求得x1+x2的表达式,表示出|AF|•|BF|建立等式求得p,则抛物线方程可得.再由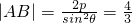 ,得
,得 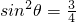 ,从而利用特殊角的三角函数求出直线AB的斜率,由点斜式方程写出AB方程.
,从而利用特殊角的三角函数求出直线AB的斜率,由点斜式方程写出AB方程.
点评:本题主要考查了抛物线的应用、直线的点斜式方程等基础知识,考查运算求解能力,考查化归与转化思想.对于抛物线的焦点弦问题常借助抛物线的定义来解决,属于基础题.
则
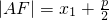 ,
,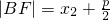 ,…(2分)
,…(2分)则
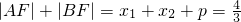 ,
,∴
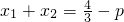 ,…(4分)
,…(4分)而若设过焦点(
 ,0)的直线斜率存在且不为0,则可设AB的方程为:y=k(x-
,0)的直线斜率存在且不为0,则可设AB的方程为:y=k(x- )
)又因为A,B两点是直线AB与抛物线的交点,则
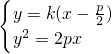 ,?x2-(
,?x2-( +p)x+
+p)x+ =0
=0∴
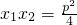 ,
,由
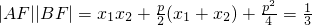 .
.得
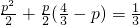 ,…(6分)
,…(6分)即
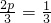 ,
,∴
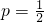 ,
,抛物线方程为y2=x.…(8分)
设直线AB的倾斜角为θ,
又根据两点间的距离公式得:|AB|2=(y2-y1)2+(x2-x1)2=(tan2θ+1)(x2-x1)2
由于直线AB过点(
 ,0),设直线AB为y=tanθ(x-
,0),设直线AB为y=tanθ(x- ),
),联立得到:tan2θx2-(tan2θ+2)px+
 p2tan2θ=0
p2tan2θ=0那么(x2-x1)2
=(x2+x1)2-4x1x 2
=(
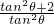 ×p)2-4×
×p)2-4×
=4p2(tan2θ+1)×
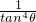
那么|AB|2=(tan2θ+1)(x2-x1)2
=(tan2θ+1)×4p2(tan2θ+1)×
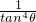
=
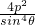 .
.∴
 ,
,由
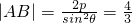 ,得
,得 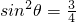 ,
,∴
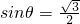 ,∴θ=600或1200,
,∴θ=600或1200,得
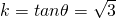 ,
,所以AB方程为
 .…(12分)
.…(12分)分析:设出A,B两点的坐标,根据抛物线定义可分别表示出|AF|和|BF|,进而可求得|AF|+|BF|求得x1+x2的表达式,表示出|AF|•|BF|建立等式求得p,则抛物线方程可得.再由
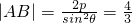 ,得
,得 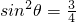 ,从而利用特殊角的三角函数求出直线AB的斜率,由点斜式方程写出AB方程.
,从而利用特殊角的三角函数求出直线AB的斜率,由点斜式方程写出AB方程.点评:本题主要考查了抛物线的应用、直线的点斜式方程等基础知识,考查运算求解能力,考查化归与转化思想.对于抛物线的焦点弦问题常借助抛物线的定义来解决,属于基础题.

练习册系列答案
相关题目
 如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2).
如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2).