��Ŀ����
����ԲE1��
+
=1����ԲE2��
+
=1����
=
=m(m��0)�������������Բ���ƣ�m�����Ʊȣ�
���������2��
)������Բ
+
=1���Ƶ���Բ�ķ��̣�
�������ԭ���һ������l�ֱ��루���е�����Բ����A��B���㣨��A���߶�OB�ϣ���
����P���߶�AB�ϵ�һ�㣬��|OA|��|OP|��|OB|�ɵȱ����У���P��Ĺ켣���̣�
����|OA|•|OB|�����ֵ����Сֵ��
| x2 | ||
|
| y2 | ||
|
| x2 | ||
|
| y2 | ||
|
| a2 |
| a1 |
| b2 |
| b1 |
���������2��
| 6 |
| x2 |
| 4 |
| y2 |
| 2 |
�������ԭ���һ������l�ֱ��루���е�����Բ����A��B���㣨��A���߶�OB�ϣ���
����P���߶�AB�ϵ�һ�㣬��|OA|��|OP|��|OB|�ɵȱ����У���P��Ĺ켣���̣�
����|OA|•|OB|�����ֵ����Сֵ��
�����������������Բ
+
=1���Ƶ���Բ�ķ���Ϊ��
+
=1�������Ŀ���������a2=16��b2=8��
���ٶԹ�ԭ���һ������l��б�ʷִ����벻���ڽ������ۣ�������ʱ����õ�P�����꣬����ʱ���ֱ��l�ķ���Ϊ��y=kx��P��x��y������A��x1��y1����B��x2��y2����
���Ӷ��ɵ�
��������
|OA|=
��ͬ��|OB|=
���ֵ�P��l�ϣ���k=
�����뼴�����P��Ĺ켣���̣�
���ɢٿ�֪����l��б�ʲ�����ʱ��|OA|•|OB|=4����l��б�ʴ���ʱ�������|OA|•|OB|=4+
���Ӷ������|OA|•|OB|�����ֵ����Сֵ��
| x2 |
| 4 |
| y2 |
| 2 |
| x2 | ||
|
| y2 | ||
|
���ٶԹ�ԭ���һ������l��б�ʷִ����벻���ڽ������ۣ�������ʱ����õ�P�����꣬����ʱ���ֱ��l�ķ���Ϊ��y=kx��P��x��y������A��x1��y1����B��x2��y2����
|
|
|OA|=
2
| ||
|
4
| ||
|
| y |
| x |
���ɢٿ�֪����l��б�ʲ�����ʱ��|OA|•|OB|=4����l��б�ʴ���ʱ�������|OA|•|OB|=4+
| 4 |
| 1+2k2 |
����⣺��������
+
=1���Ƶ���Բ�ķ���
+
=1��
����
����3�֣�
���a2=16��b2=8��
������
+
=1������4�֣�
���� �ٵ�����l��б�ʲ�����ʱA(0����
)��B(0����2
)��
���P����P��0��y0������y02=4��y0=��2����P��0����2��������5�֣�
������l��б�ʴ���ʱ�����䷽��y=kx��P��x��y��
��A��x1��y1����B��x2��y2����
��
��|OA|=
ͬ��|OB|=
����7�֣�
�ֵ�P��l�ϣ���k=
������x2+y2=
=
=
��
��������
+
=1��
�֡ߣ�0����2���ʺϷ��̣�
��������Բ�ķ�����
+
=1������9�֣�
���ɢٿ�֪����l��б�ʲ�����ʱ��|OA|•|OB|=
•2
=4����l��б�ʴ���ʱ��|OA|•|OB|=
=4+
��
��4��|OA|•|OB|��8������11�֣�
���ϣ�|OA|•|OB|�����ֵ��8����Сֵ��4������12�֣�
| x2 |
| 4 |
| y2 |
| 2 |
| x2 | ||
|
| y2 | ||
|
����
|
���a2=16��b2=8��
������
| x2 |
| 16 |
| y2 |
| 8 |
���� �ٵ�����l��б�ʲ�����ʱA(0����
| 2 |
| 2 |
���P����P��0��y0������y02=4��y0=��2����P��0����2��������5�֣�
������l��б�ʴ���ʱ�����䷽��y=kx��P��x��y��
��A��x1��y1����B��x2��y2����
|
��
|
��|OA|=
2
| ||
|
4
| ||
|
�ֵ�P��l�ϣ���k=
| y |
| x |
| 8(1+k2) |
| 1+2k2 |
8(1+
| ||
1+2
|
| 8(x2+y2) |
| x2+2y2 |
��������
| x2 |
| 8 |
| y2 |
| 4 |
�֡ߣ�0����2���ʺϷ��̣�
��������Բ�ķ�����
| x2 |
| 8 |
| y2 |
| 4 |
���ɢٿ�֪����l��б�ʲ�����ʱ��|OA|•|OB|=
| 2 |
| 2 |
| 8(1+b2) |
| 1+2k2 |
| 4 |
| 1+2k2 |
��4��|OA|•|OB|��8������11�֣�
���ϣ�|OA|•|OB|�����ֵ��8����Сֵ��4������12�֣�
���������⿼��ֱ����Բ���ߵ��ۺ����⣬���ؿ�����Բ�ı����̣����η����Ĺ켣���ѵ�����ֱ������Բ���ۺϷ�����Ӧ�ã�˼ά��̣����㸴�ӣ��Ѷȴ��������⣮

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ����֪��ԲE1����Ϊ
��ͼ����֪��ԲE1����Ϊ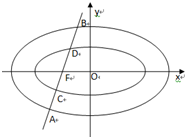 ��֪��ԲE1��
��֪��ԲE1��